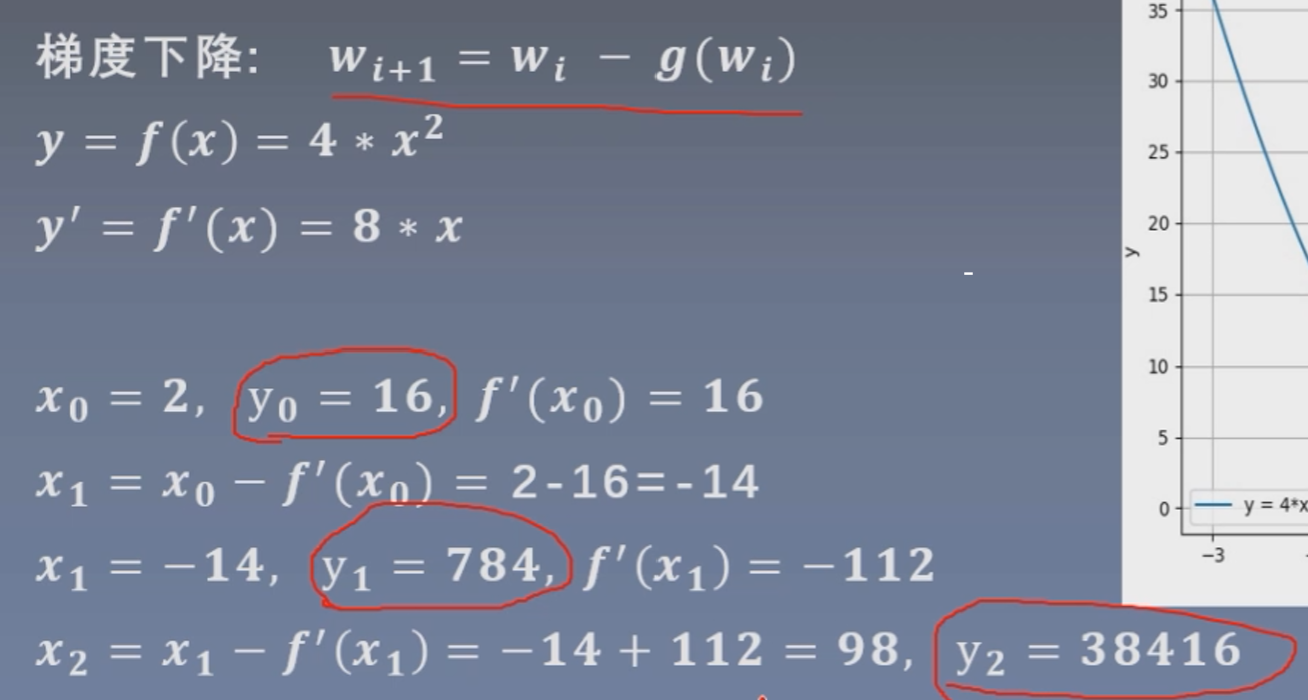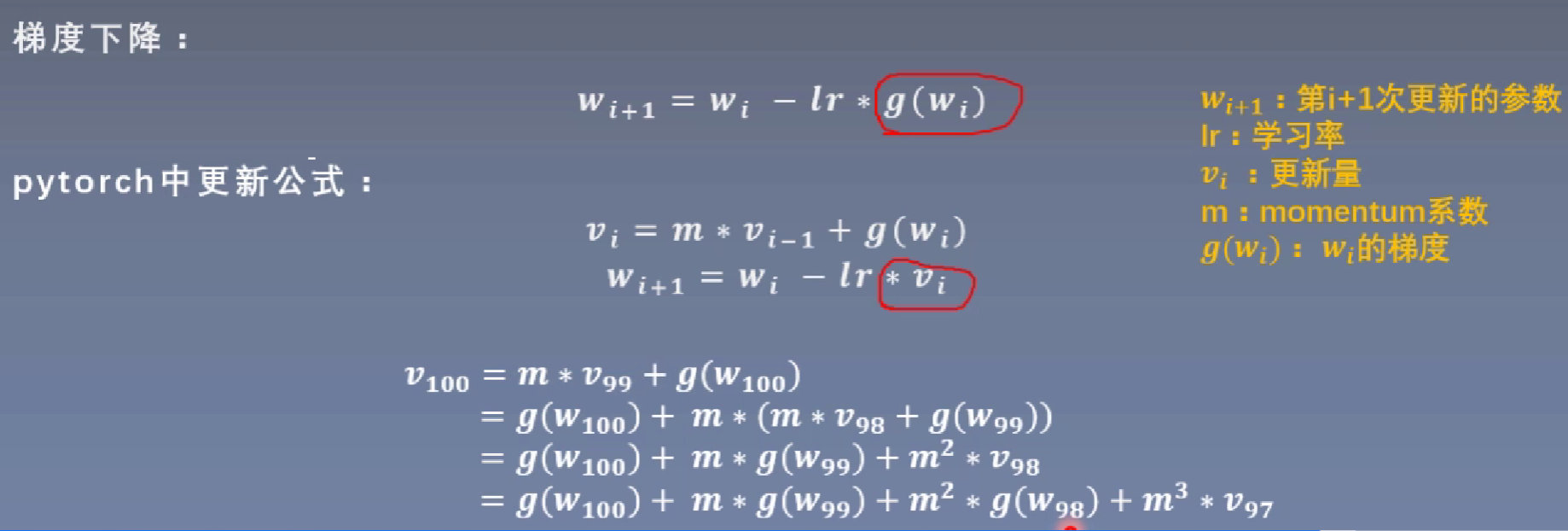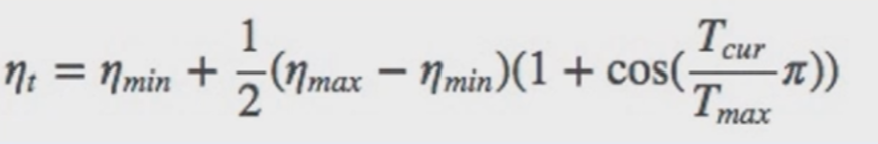当前所在位置： 主页 > 耀世新闻 > 公司新闻

Pytorch中的优化器Optimizer_1

的优化器：管理并更新模型中可学习参数的值，使得模型输出更接近真实标签

导数：函数在指定坐标轴上的变化率
方向导数：指定方向上的变化率（二元及以上函数，偏导数）
梯度：一个向量，方向是使得方向导数取得最大值的方向

参数

基本方法：

特性：张量梯度不会自动清零

使用代码帮助理解和学习

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import os
import torch
import torch.optim as optim


BASE_DIR=os.path.dirname(os.path.abspath(__file__))


weight=torch.randn((2, 2), requires_grad=True)
weight.grad=torch.ones((2, 2))

# 需要传入一个可迭代对象
optimizer=optim.SGD([weight], lr=1)

print("weight before step:{}".format(weight.data))
optimizer.step()
print("weight after step:{}".format(weight.data))

weight before step:tensor([[-0.0606, -0.3197],
        [ 1.4949, -0.8007]])
weight after step:tensor([[-1.0606, -1.3197],
        [ 0.4949, -1.8007]])


上面学习率是1，把学习率改为0.1试一下

1
2
3
4
5
6
optimizer=optim.SGD([weight], lr=0.1)

weight before step:tensor([[ 0.3901,  0.2167],
        [-0.3428, -0.7151]])
weight after step:tensor([[ 0.2901,  0.1167],
        [-0.4428, -0.8151]])

接着上面的代码，我们再看一下方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# add_param_group方法
print("optimizer.param_groups is 
{}".format(optimizer.param_groups))

w2=torch.randn((3, 3), requires_grad=True)
optimizer.add_param_group({"params": w2, "lr": 0.0001})
print("optimizer.param_groups is
{}".format(optimizer.param_groups))

optimizer.param_groups is 
[{'params': [tensor([[ 0.1749, -0.2018],
        [ 0.0080,  0.3517]], requires_grad=True)], 'lr': 0.1, 'momentum': 0, 'dampening': 0, 'weight_decay': 0, 'nesterov': False}]

optimizer.param_groups is
[{'params': [tensor([[ 0.1749, -0.2018],
        [ 0.0080,  0.3517]], requires_grad=True)], 'lr': 0.1, 'momentum': 0, 'dampening': 0, 'weight_decay': 0, 'nesterov': False}, 
 {'params': [tensor([[ 0.4538, -0.8521, -1.3081],
        [-0.0158, -0.2708,  0.0302],
        [-0.3751, -0.1052, -0.3030]], requires_grad=True)], 'lr': 0.0001, 'momentum': 0, 'dampening': 0, 'weight_decay': 0, 'nesterov': False}]

关于、、、这几个方法比较简单就不再赘述。

learning_rate学习率

这里学习率为1，可以看到并没有达到梯度下降的效果，反而y值越来越大，这是因为更新的步伐太大。

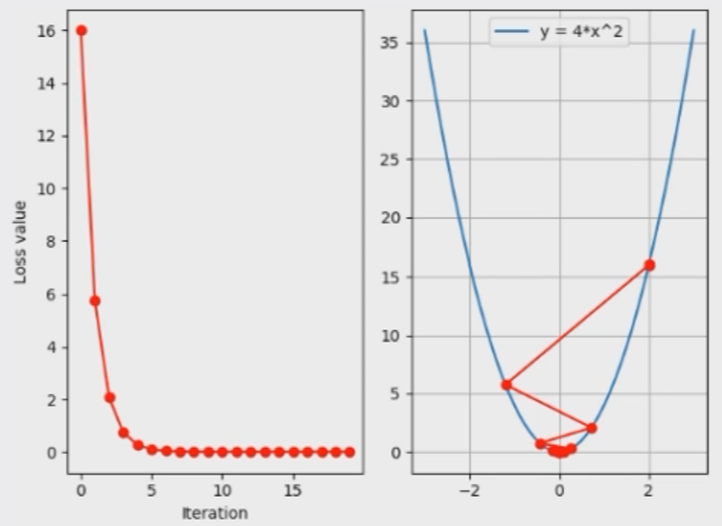
我们以这个函数举例，将y值作为要优化的损失值，那么梯度下降的过程就是为了找到y的最小值（即此函数曲线的最小值）；如果我们把学习率设置为0.2，就可以得到这样一个梯度下降的图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def func(x):
    return torch.pow(2*x, 2)

x=torch.tensor([2.], requires_grad=True)
iter_rec, loss_rec, x_rec=list(), list(), list()
lr=0.2
max_iteration=20

for i in range(max_iteration):
    y=func(x)
    y.backward()

    print("iter:{}, x:{:8}, x.grad:{:8}, loss:{:10}".format(
        i, x.detach().numpy()[0], x.grad.detach().numpy()[0], y.item()
    ))
    x_rec.append(x.item())
    x.data.sub_(lr * x.grad)
    x.grad.zero_()
    iter_rec.append(i)
    loss_rec.append(y.item())

plt.subplot(121).plot(iter_rec, loss_rec, '-ro')
plt.xlabel("Iteration")
plt.ylabel("Loss value")

x_t=torch.linspace(-3, 3, 100)
y=func(x_t)
plt.subplot(122).plot(x_t.numpy(), y.numpy(), label="y=4*x^2")
plt.grid()

y_rec=[func(torch.tensor(i)).item() for i in x_rec]
plt.subplot(122).plot(x_rec, y_rec, '-ro')
plt.legend()
plt.show()

这里其实存在一个下降速度更快的学习率，那就是0.125，一步就可以将loss更新为0，这是因为我们已经了这个函数表达式，而在实际神经网络模型训练的过程中，是不知道所谓的函数表达式的，所以只能选取一个相对较小的学习率，然后以训练更多的迭代次数来达到最优的loss。

动量（Momentum，又叫冲量）

结合当前梯度与上一次更新信息，用于当前更新

为什么会出现动量这个概念？

当学习率比较小时，往往更新比较慢，通过引入动量，使得后续的更新受到前面更新的影响，可以更快的进行梯度下降。

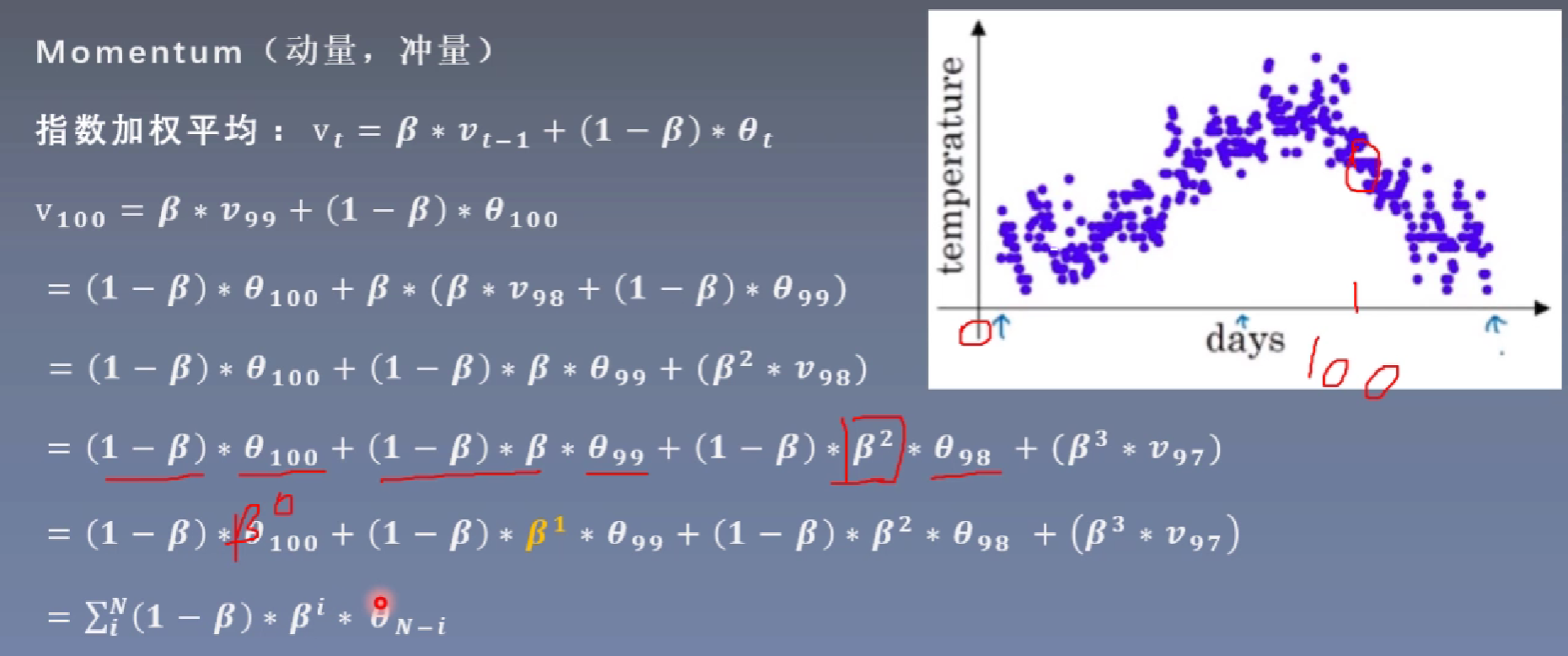
指数加权平均：当前时刻的平均值（Vt）与当前参数值（θ）和前一时刻的平均值（Vt-1）的关系。

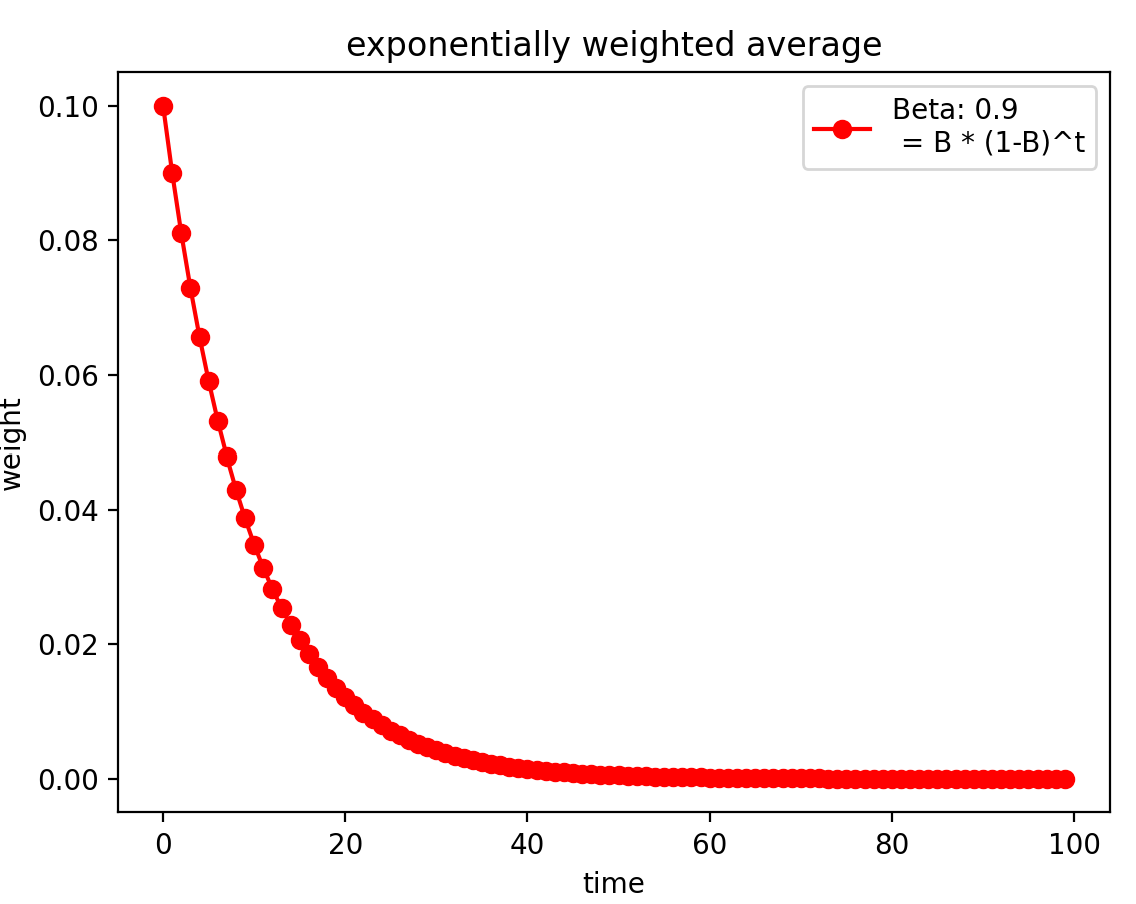
根据上述公式进行迭代展开，因为0<β<1，当前时刻的平均值受越近时刻的影响越大（更近的时刻其所占的权重更高），越远时刻的影响越小，我们可以通过下面作图来看到这一变化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import numpy as np
import matplotlib.pyplot as plt


def exp_w_func(beta, time_list):
    return [(1-beta) * np.power(beta, exp) for exp in time_list]


beta=0.9
num_point=100
time_list=np.arange(num_point).tolist()

weights=exp_w_func(beta, time_list)

plt.plot(time_list, weights, '-ro', label="Beta: {}
=B * (1-B)^t".format(beta))
plt.xlabel("time")
plt.ylabel("weight")
plt.legend()
plt.title("exponentially weighted average")
plt.show()

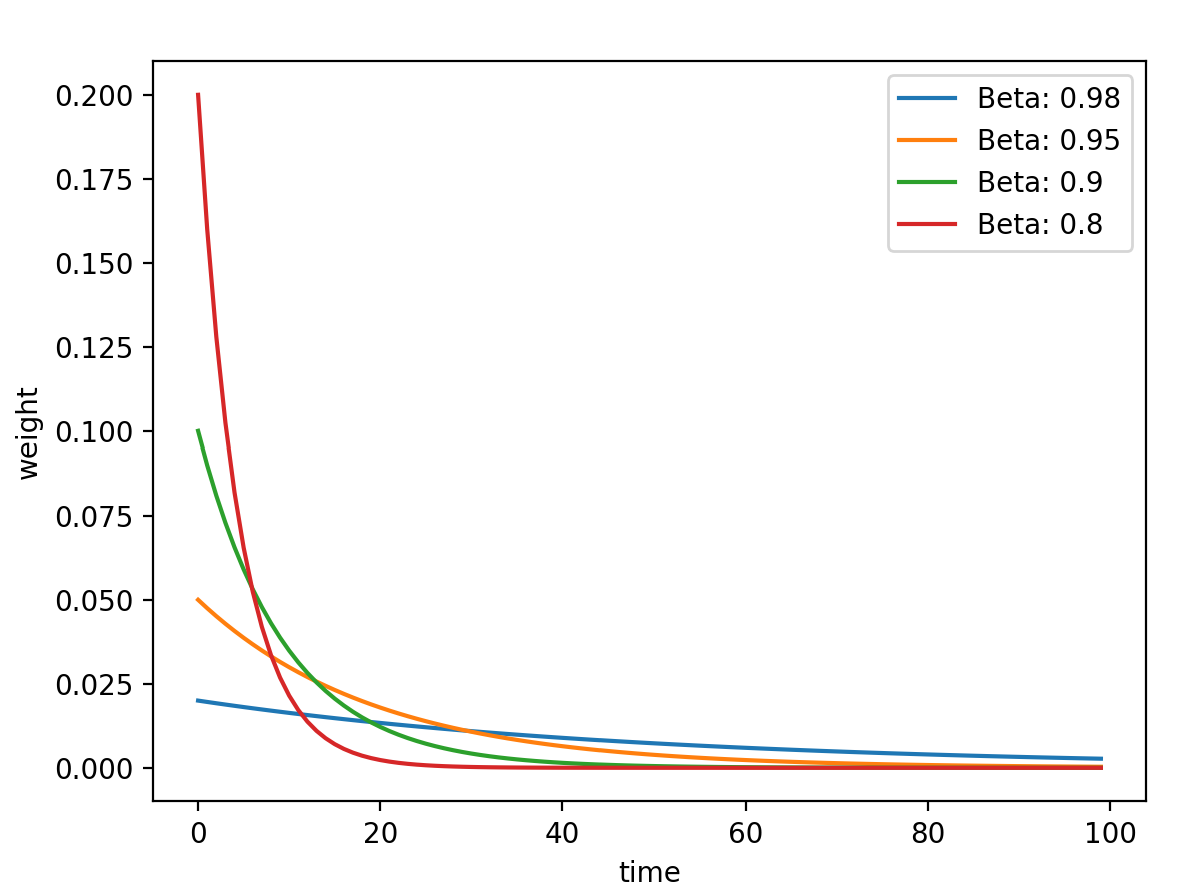
这里β是一个超参数，设置不同的值，其对于过去时刻的权重计算如下图

1
2
3
4
5
6
7
8
beta_list=[0.98, 0.95, 0.9, 0.8]
w_list=[exp_w_func(beta, time_list) for beta in beta_list]
for i, w in enumerate(w_list):
    plt.plot(time_list, w, label="Beta: {}".format(beta_list[i]))
    plt.xlabel("time")
    plt.ylabel("weight")
plt.legend()
plt.show()

从图中可以得到这一结论：β值越小，记忆周期越短，β值越大，记忆周期越长。

中带有momentum参数的更新公式

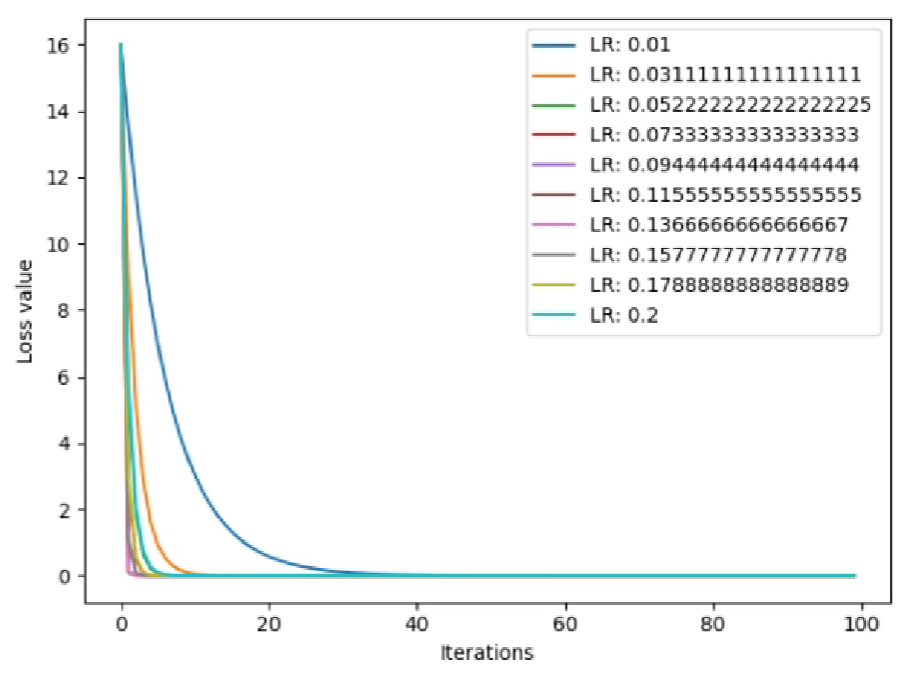
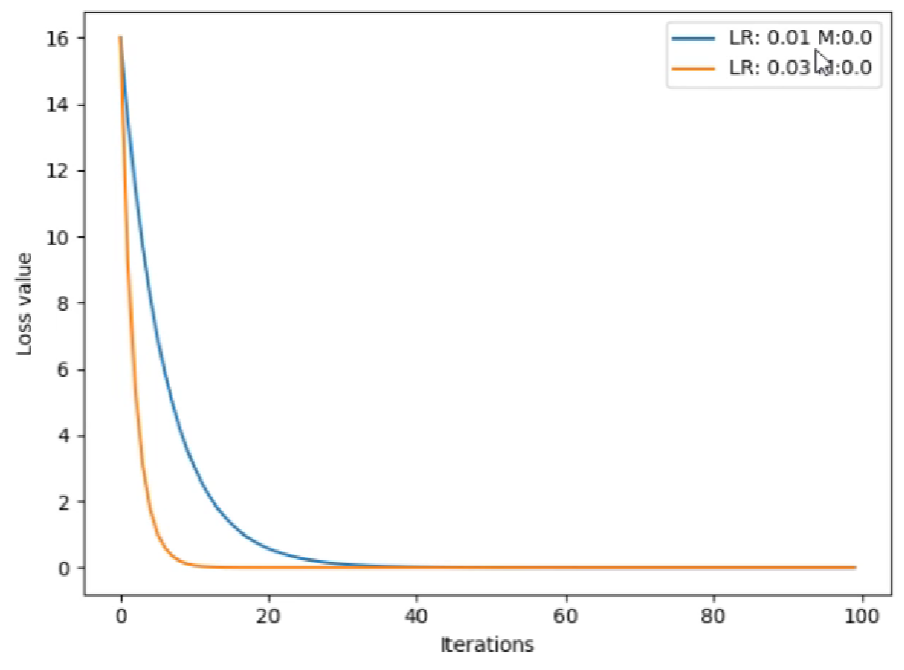
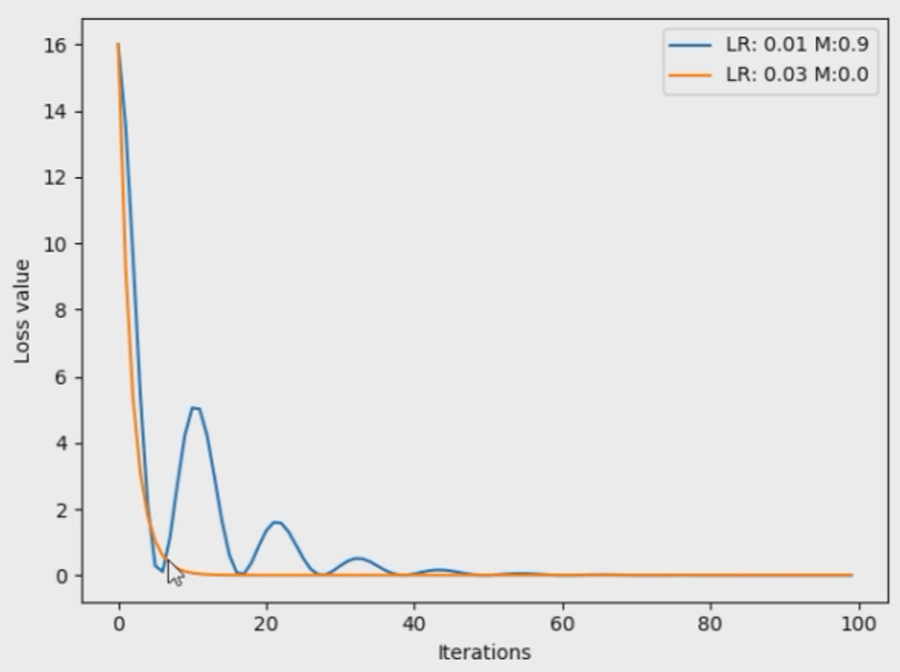
对于这个例子，在没有momentum时，我们对比学习率分别为0.01和0.03会发现，0.03收敛的更快。

如果我们给learning_rate=0.01增加momentum参数，会发现其可以先一步0.03的学习率到达loss的较小值，但是因为动量较大的因素，在达到了最小值后还会反弹到一个大的值。

中的优化器

主要参数：

：自适应学习率梯度下降法

：Adagrad的改进

：Adagrad的改进

：RMSprop结合Momentum

：Adam增加学习率上限

：稀疏版的Adam

：随机平均梯度下降

：弹性反向传播

：BFGS的改进

前期学习率大，后期学习率小

中调整学习率的基类

主要属性：

主要方法：

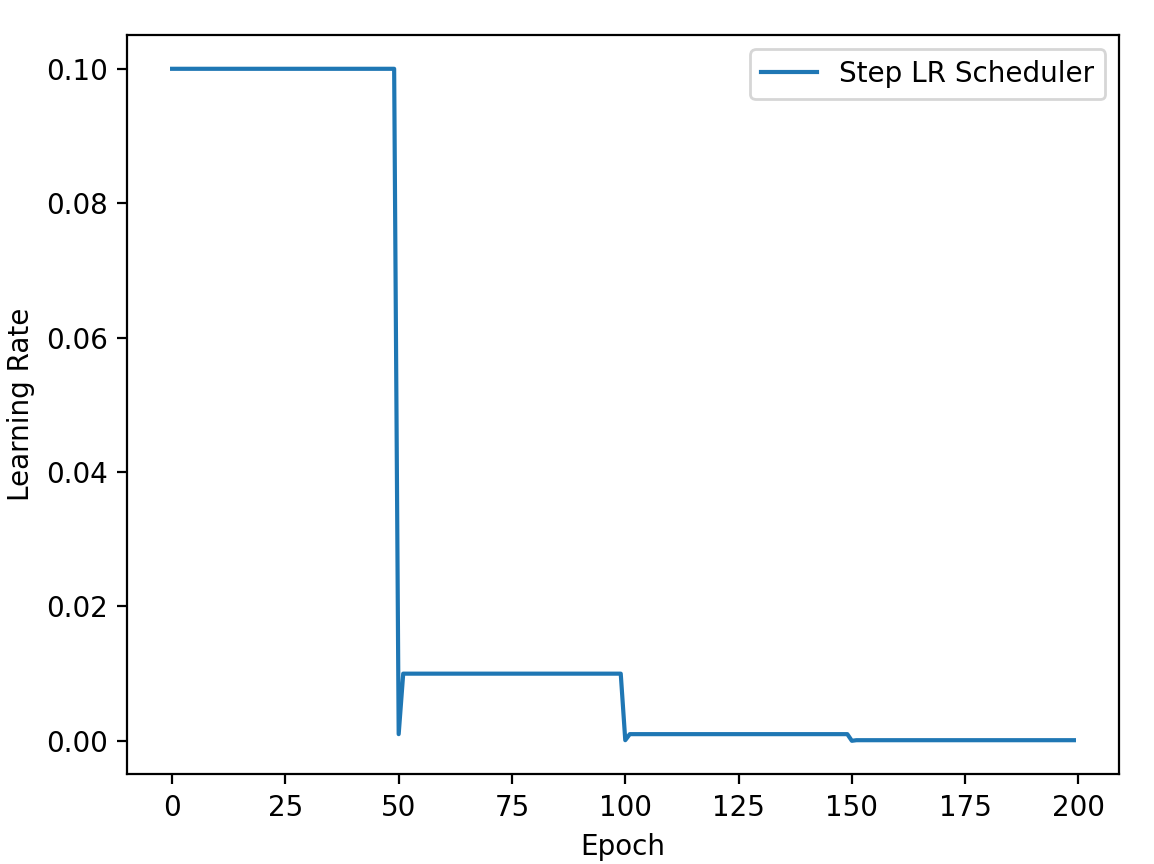
等间隔调整学习率

主要参数：

调整方式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import torch
import torch.optim as optim
import matplotlib.pyplot as plt


LR=0.1
iteration=10
max_epoch=200

weights=torch.randn((1,), requires_grad=True)
target=torch.zeros((1, ))

optimizer=optim.SGD([weights], lr=LR, momentum=0.9)


scheduler_lr=optim.lr_scheduler.StepLR(optimizer, step_size=50, gamma=0.1)  # 设置学习率下降策略

lr_list, epoch_list=list(), list()
for epoch in range(max_epoch):
    lr_list.append(scheduler_lr.get_lr())
    epoch_list.append(epoch)

    for i in range(iteration):
        loss=torch.pow((weights-target), 2)
        loss.backward()
        optimizer.step()
        optimizer.zero_grad()

    scheduler_lr.step()

plt.plot(epoch_list, lr_list, label='Step LR Scheduler')
plt.xlabel('Epoch')
plt.ylabel('Learning Rate')
plt.legend()
plt.show()

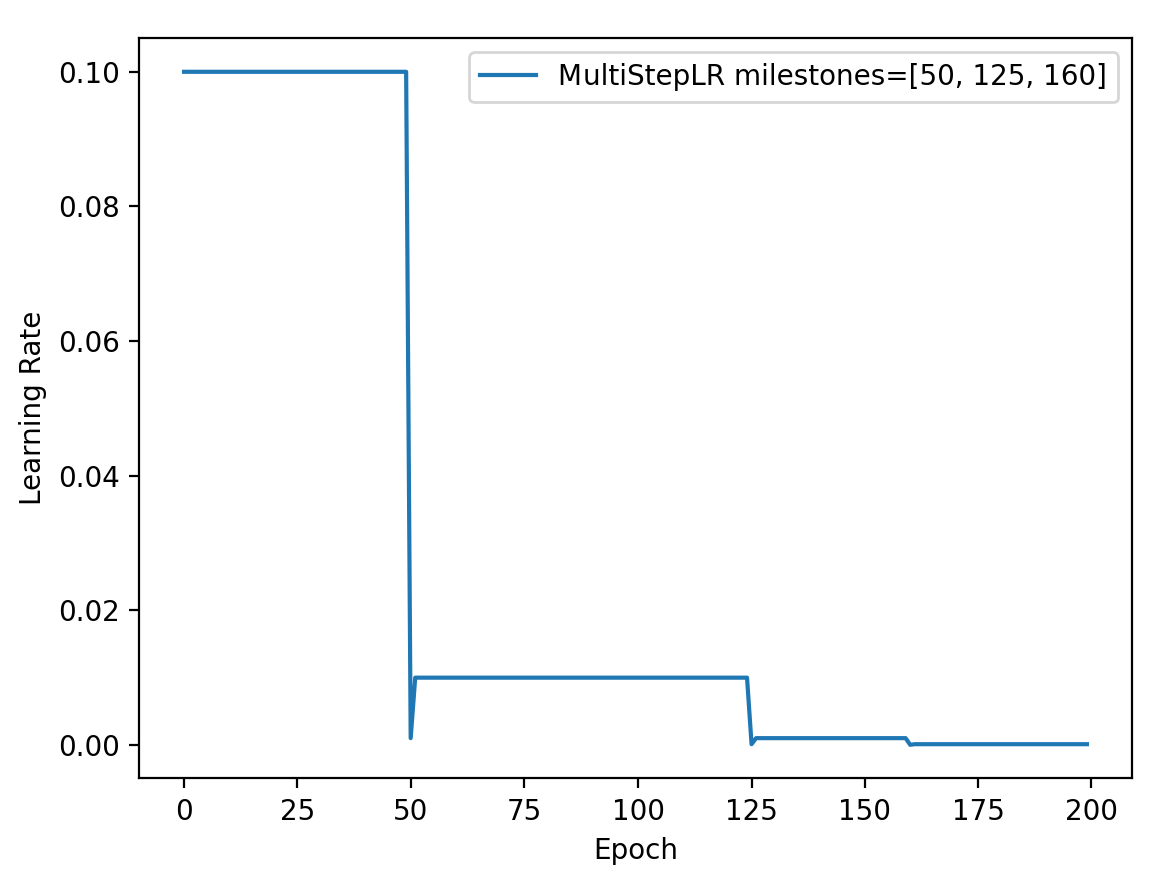
功能：按给定间隔调整学习率

主要参数：

调整方式：

1
2
3
# MultiStepLR
milestones=[50, 125, 160]
scheduler_lr=optim.lr_scheduler.MultiStepLR(optimizer, milestones=milestones, gamma=0.1)

只需要改变这里代码，其他部分与中基本一致

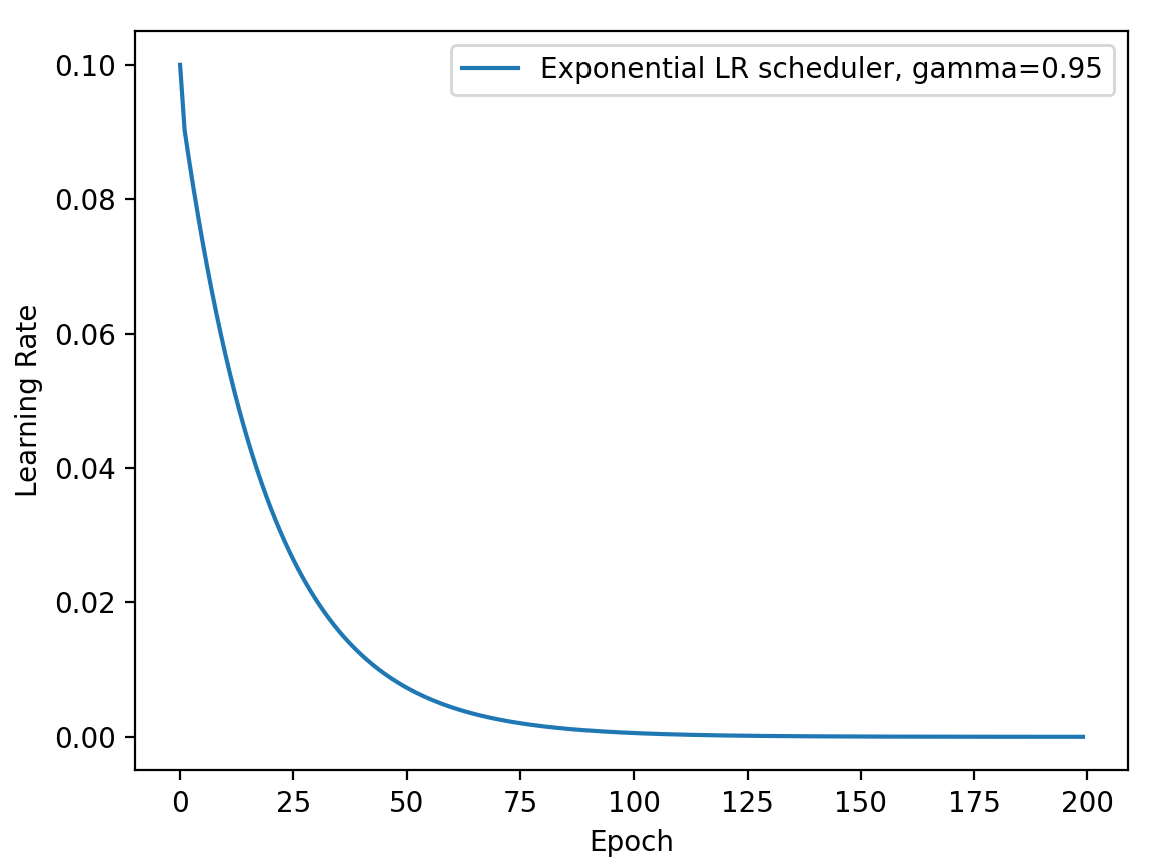
功能：按指数衰减调整学习率

主要参数：

调整方式：

1
2
3
# Exponential LR
gamma=0.95
scheduler_lr=optim.lr_scheduler.ExponentialLR(optimizer, gamma=gamma)

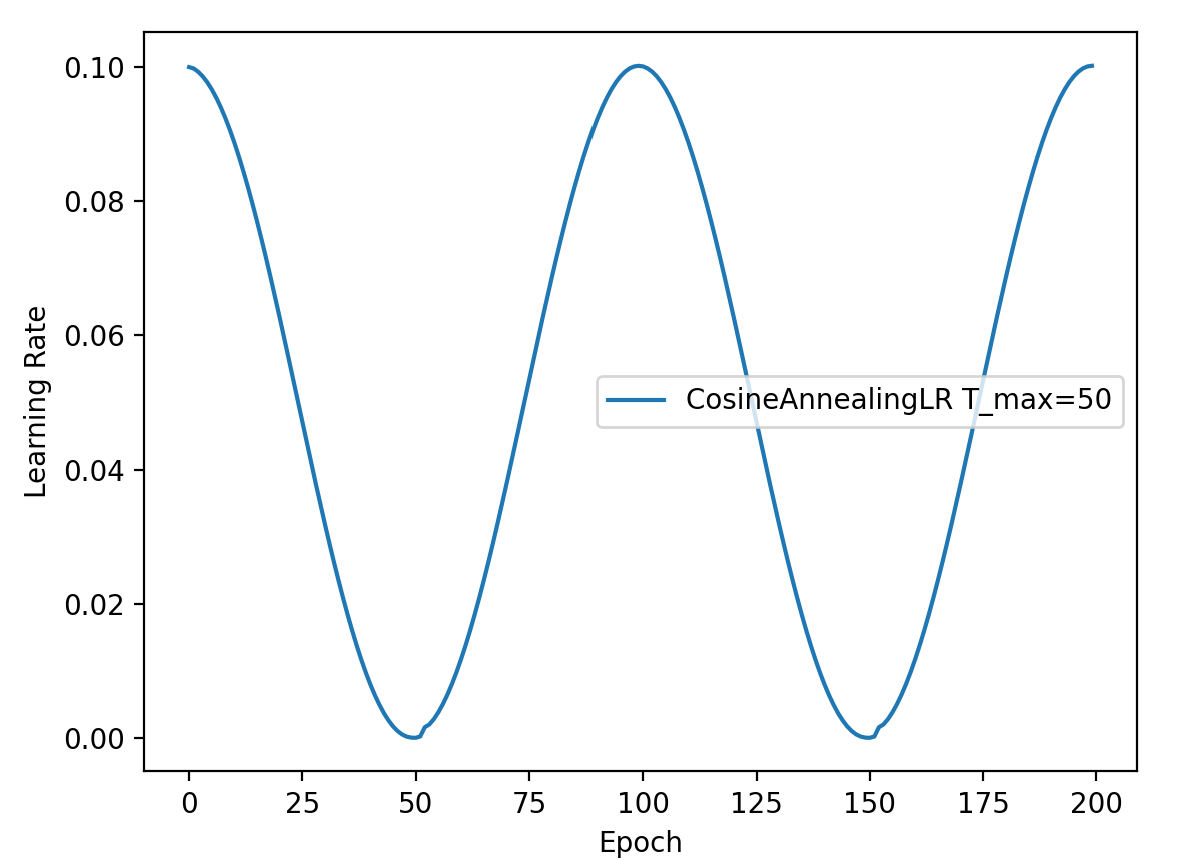
功能：余弦周期调整学习率

主要参数：

调整方式：

1
2
3
# CosineAnnealingLR
t_max=50
scheduler_lr=optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=t_max, eta_min=0)

功能：监控指标，当指标不再变化则调整学习率

主要参数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# Reduce LR on Plateau
loss_value=0.5
accuray=0.9

factor=0.1
mode='min'
patience=10
cooldown=10
min_lr=1e-4
verbose=True

scheduler_lr=optim.lr_scheduler.ReduceLROnPlateau(optimizer, factor=factor, mode=mode, patience=patience,
                                                    cooldown=cooldown, min_lr=min_lr, verbose=verbose)
for epoch in range(max_epoch):
    for i in range(iteration):
        optimizer.step()
        optimizer.zero_grad()
    # if epoch==5:
        # loss_value=0.4

    # 把要监控的指标传进去
    scheduler_lr.step(loss_value)

Epoch    12: reducing learning rate of group 0 to 1.0000e-02.
Epoch    33: reducing learning rate of group 0 to 1.0000e-03.
Epoch    54: reducing learning rate of group 0 to 1.0000e-04.

功能：自定义调整策略

主要参数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# lambda LR

lr_init=0.1
weights_1=torch.randn((6, 3, 5, 5))
weights_2=torch.ones((5, 5))

optimizer=optim.SGD([
    {'params': [weights_1]},
    {'params': [weights_2]}
], lr=lr_init)

lambda1=lambda epoch: 0.1 ** (epoch // 20)
lambda2=lambda epoch: 0.95 ** epoch


scheduler=torch.optim.lr_scheduler.LambdaLR(optimizer, lr_lambda=[lambda1, lambda2])

lr_list, epoch_list=list(), list()
for epoch in range(max_epoch):
    for i in range(iteration):
        optimizer.step()
        optimizer.zero_grad()
    scheduler.step()

    lr_list.append(scheduler.get_lr())
    epoch_list.append(epoch)

    print('epoch: {:5d}, lr:{}'.format(epoch, scheduler.get_lr()))

transformer包中的

我们都知道模型在开始时可以采用较大的学习率，然后快速的收敛，随着模型训练到后期需要减少学习率才能使得模型进一步学习，如果持续使用较大的学习率会使得模型最后无法走到一个局部的最优点，所以有一种叫做的学习率调整策略，偏向于前期采用较大的学习率，后期逐渐减小学习率。

在transformer包中就已经封装了类似的方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import transformers

def _get_scheduler(self, optimizer, scheduler: str, warmup_steps: int, t_total: int):
        """
        Returns the correct learning rate scheduler
        """
        scheduler=scheduler.lower()
        if scheduler=='constantlr':
            return transformers.get_constant_schedule(optimizer)
        elif scheduler=='warmupconstant':
            return transformers.get_constant_schedule_with_warmup(optimizer, num_warmup_steps=warmup_steps)
        elif scheduler=='warmuplinear':
            return transformers.get_linear_schedule_with_warmup(optimizer, num_warmup_steps=warmup_steps, num_training_steps=t_total)
        elif scheduler=='warmupcosine':
            return transformers.get_cosine_schedule_with_warmup(optimizer, num_warmup_steps=warmup_steps, num_training_steps=t_total)
        elif scheduler=='warmupcosinewithhardrestarts':
            return transformers.get_cosine_with_hard_restarts_schedule_with_warmup(optimizer, num_warmup_steps=warmup_steps, num_training_steps=t_total)
        else:
            raise ValueError("Unknown scheduler {}".format(scheduler))

这里我们详细看一下来进一步理解该方法是如何调整学习率的。

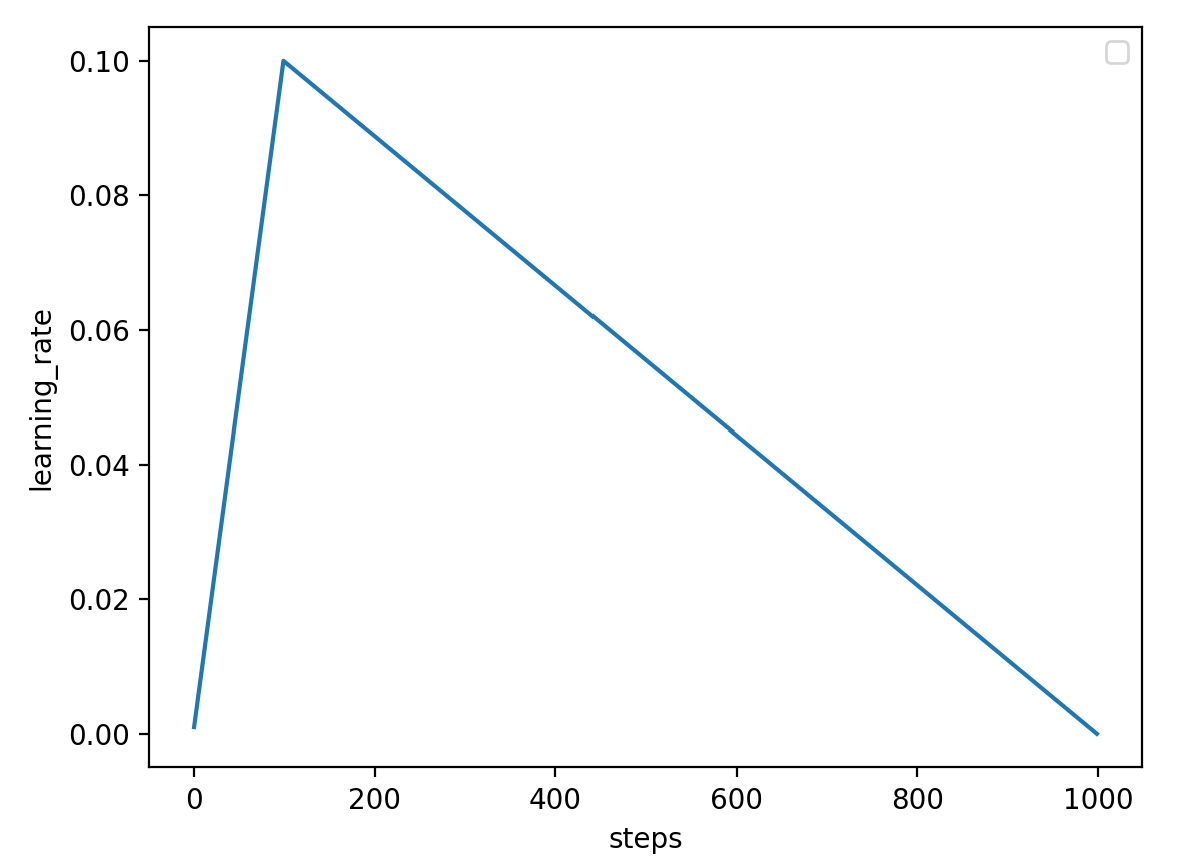
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from transformers import AdamW, get_linear_schedule_with_warmup

lr_init=0.1
weights_1=torch.randn((6, 3, 5, 5))

optimizer=AdamW([{"params": [weights_1]}], lr=lr_init, eps=1e-4)
epochs=10
batch_size=32
total_steps=1000
warm_up_ratio=0.1  # 定义要预热的step
scheduler=get_linear_schedule_with_warmup(optimizer,
                                            num_warmup_steps=warm_up_ratio * total_steps,
                                            num_training_steps=total_steps)
lr_list=[]
for epoch in range(epochs):
    for i in range(100):
        optimizer.step()
        scheduler.step()
        optimizer.zero_grad()
        lr_list.append(scheduler.get_lr())


plt.plot(range(total_steps), lr_list)
plt.xlabel("steps")
plt.ylabel("learning_rate")
plt.legend()
plt.show()

可以看到，根据我们预先设置在总的训练步数的一个比例上，这里是1000的10%，那就是前100步，学习率是从0线性的增长到我们预先设定的学习率，之后线性的减小到0。

当参数设置为0时，learning rate没有预热的上升过程，只有从初始设定的learning rate 逐渐衰减到0的过程，也就是get_constant_schedule方法。

那其实还有一个问题，类似Adam之类的优化器，本身不是自适应学习率的吗？为什么还需要再引入相关方法来调整学习率呢？

因为常用的神经网络优化器Adam的自适应学习率并不是真正意义上的自适应。

从统计的角度看，Adam的自适应原理也是根据统计对梯度进行修正，但依然离不开前面设置的学习率。如果学习率设置的过大，则会导致模型发散，造成收敛较慢或陷入局部最小值点，因为过大的学习率会在优化过程中跳过最优解或次优解。
所以Adam在调整学习率时也是根据预先设置的学习率来调整的，如果我们本身可以控制学习率的变化，再通过Adam来微调可以得到更好的效果。


版权所有：Copyright © 2002-2022 耀世娱乐全球认证招商站 版权所有    ICP备案号：粤IP********

平台注册入口