机器学习中的高性能计算（一）CPU优化

本文涉及到的代码，见 zackchen/ParallelProgrammingInAction

简单谈一下我们为什么需要高性能编程。其实原因很简单，那就是我们希望计算尽量快。

在机器学习领域，模型训练和推理过程中都有大量的计算，尤其是大量的向量和矩阵计算。比如矩阵乘法（GEMM），卷积（Conv），类似Polling/Filter的算子等，这些计算有一个共同的特点就是可以利用并行编程加块计算的速度。

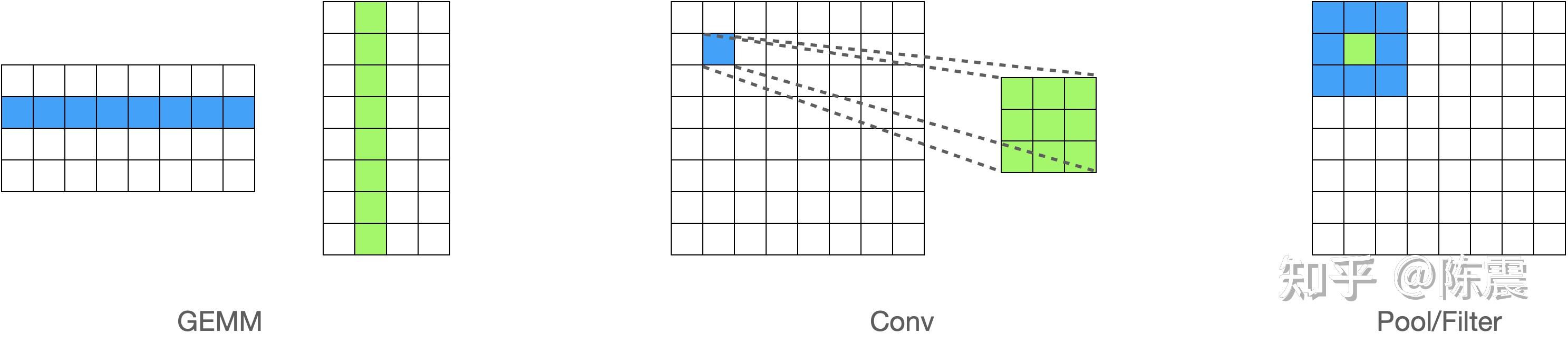
举一个最简单的例子。如果我们要对一张图片（简化为一个矩阵）进行模糊处理（Blur），最简单的一种算法就是均值模糊，又叫标准盒式过滤器（Normalized Box Filter），其方法就是对每一个元素和围绕它周围的元素求均值，周围的元素可以组成一个“盒子”或者叫“核”。

这个“盒子”的选择方法一般有两种，要么当前元素作为盒子的左上角元素（如图中浅蓝色的盒子）；要么作为盒子的中间元素（如图中灰色的盒子）。在实际编程中，还要考虑处理边界的情况（如同中深蓝色的盒子）。选择哪一种方法这里并不重要，为了简化编程，我们在接下来的编程中选择第一种。

其实，均值模糊在实现中还可以利用深度神经网络中很常用的卷积（Conv）操作，即如果我们用一个值全都是1的卷积核对每个元素进行卷积操作，可以得到相同的结果。或者从另外一个角度，卷积就是一种Filter。本文为了简单，我们接下来还是用最朴素的求和方法。

2 算法的朴素实现

对于上面这个问题，最简单的实现就是一个两层嵌套的循环，对每一个元素分别进行计算。这个代码相信计算机专业大学一年级的同学就能很快的写出来，这里不多解释了。

void blur_mat_original(const vector<vector<float>> &input,
                       vector<vector<float>> &output) {
  int height = input.size();
  int width = input[0].size();
  int right, right_right, below, below_below;
  for (int x = 0; x < width; ++x) {
    right = x + 1 >= width ? width - 1 : x + 1;
    right_right = x + 2 >= width ? width - 1 : x + 2;
    for (int y = 0; y < height; ++y) {
      below = y + 1 >= height ? height - 1 : y + 1;
      below_below = y + 2 >= height ? height - 1 : y + 2;
      output[y][x] =
          ((input[y][x] + input[y][right] + input[y][right_right]) +
           (input[below][x] + input[below][right] + input[below][right_right]) +
           (input[below_below][x] + input[below_below][right] +
            input[below_below][right_right])) / 9;
    }
  }
}

我们选择的测试矩阵大小为 8192*4096，核大小为3*3，数据类型为float32。使用gcc编译并运行，这段代码在我的机器上的执行时间是3914ms

$ g++ cpu.cpp -O0 -o cpu -std=c++11 && https://zhuanlan.zhihu.com/p/cpu

如果这是一道程序员面试题，上面的这个答案显然不能拿到高分，因为这里面有肉眼可见的重复计算。由于我们是遍历每一个元素，对其“盒子”内的元素求均值时，我们计算了9个元素的和，在遍历过程中，由于盒子间会有重叠，因此有些元素的和被重复计算了。如下图中浅绿色和深绿色的两个元素的计算，橙色部分的计算就是重复的。

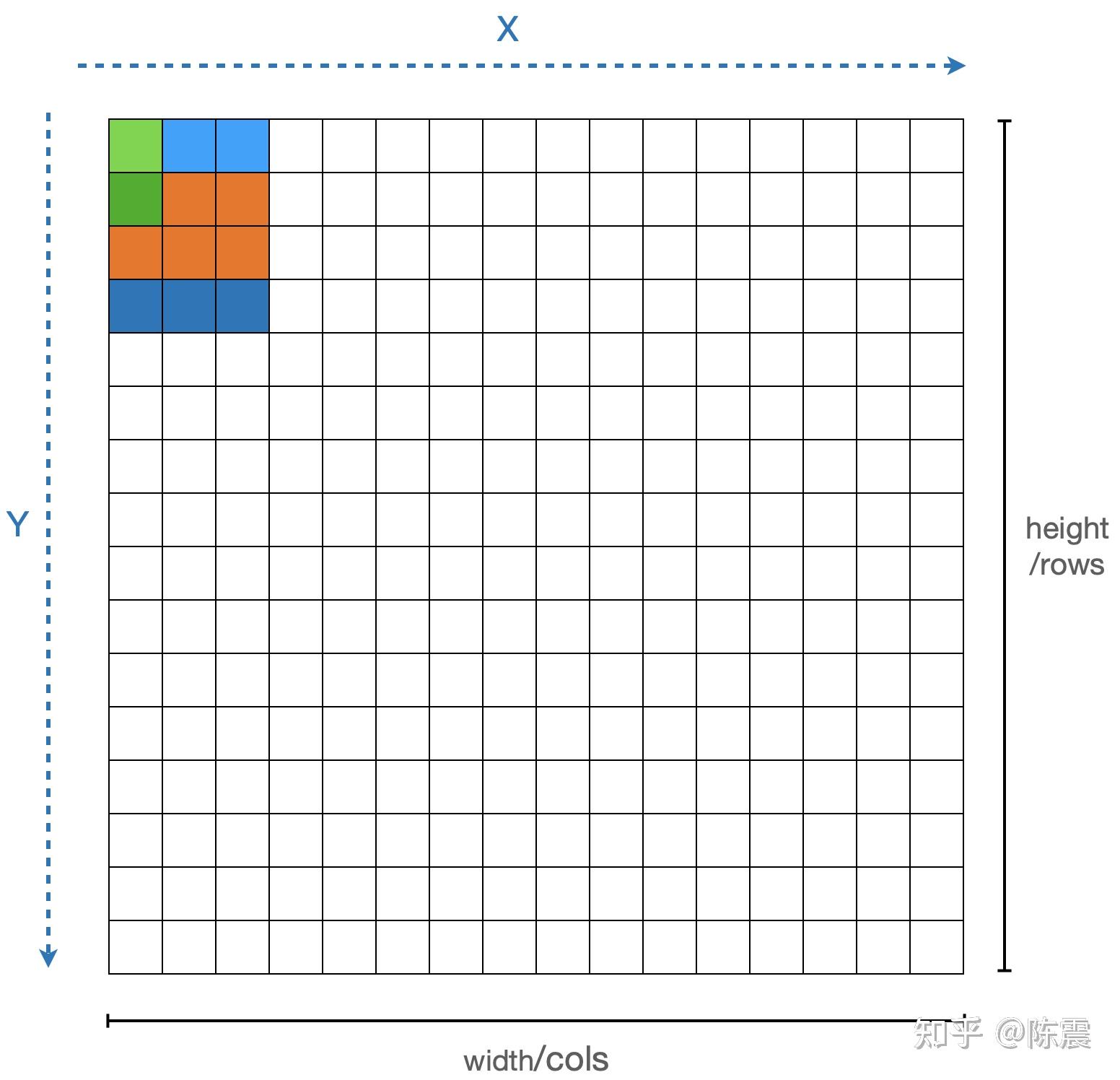
如何优化呢？

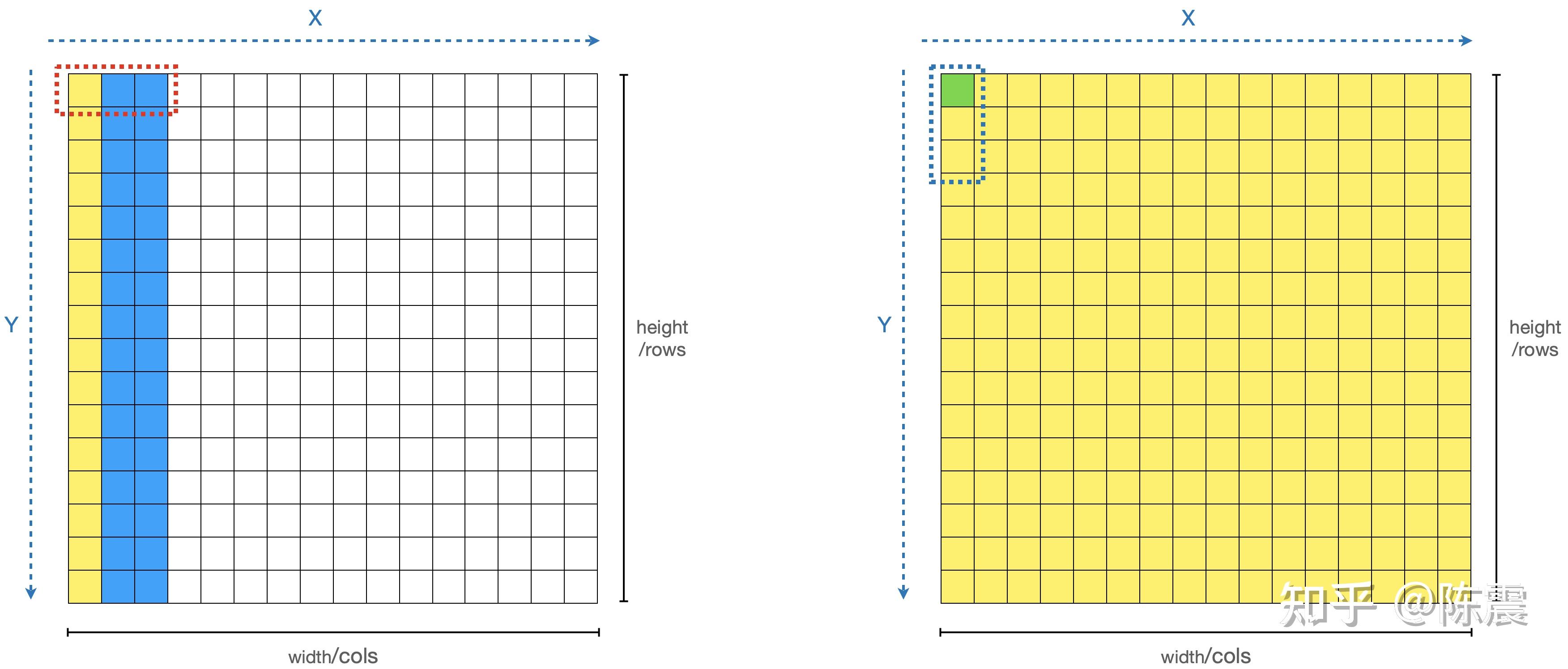
我们可以把这个计算分成两个阶段，两次遍历。第一次遍历，如左图，对每一个元素和其右边两个元素求均值并保存下来，如左图的黄色部分。等所有元素都变成黄色之后，我们进行第二次遍历，对每一个元素和其下方的两个元素求和并求均值，从而得到最终的解。

void blur_mat_redup(const vector<vector<float>> &input,
                    vector<vector<float>> &output) {
  int height = input.size();
  int width = input[0].size();
  int right, right_right, below, below_below;
  for (int x = 0; x < width; ++x) {
    for (int y = 0; y < height; ++y) {
      right = x + 1 >= width ? width - 1 : x + 1;
      right_right = x + 2 >= width ? width - 1 : x + 2;
      output[y][x] =
          (input[y][x] + input[y][right] + input[y][right_right]) / 3;
    }
  }
 
  for (int x = 0; x < width; ++x) {
    for (int y = 0; y < height; ++y) {
      below = y + 1 >= height ? height - 1 : y + 1;
      below_below = y + 2 >= height ? height - 1 : y + 2;
      output[y][x] =
          (output[y][x] + output[below][x] + output[below_below][x]) / 3;
    }
  }
}

上面是具体的代码实现，就是把原来的一个循环改成了两个循环，并充分利用了output变量的空间缓存中间结果，是一种典型的“空间换时间”的方法。再使用同样的参数和硬件配置，编译并运行后，性能果然有所提升，总时间从3914ms下降到3281ms。

如果有应届生同学在面试中写出了上面的答案，我觉得有比较大的概率会通过第一轮面试：）

上面的优化我们通过减少重复计算从而提升了代码的性能。但是，了解计算机组成原理和体系结构的同学会知道，如今的CPU的主频非常高，制约计算机性能的主要方面往往是IO的性能，尤其是内存的性能。大多数时候CPU都在等内存的数据，因此我们才会有L1缓存，L2缓存等硬件和非阻塞机制来减少CPU等待IO的时间。下图展示了从CPU到寄存器、缓存、物理内存、固态硬盘、机械硬盘等不同硬件的速度。基本上每差一级，速度都有数量级上的降低。

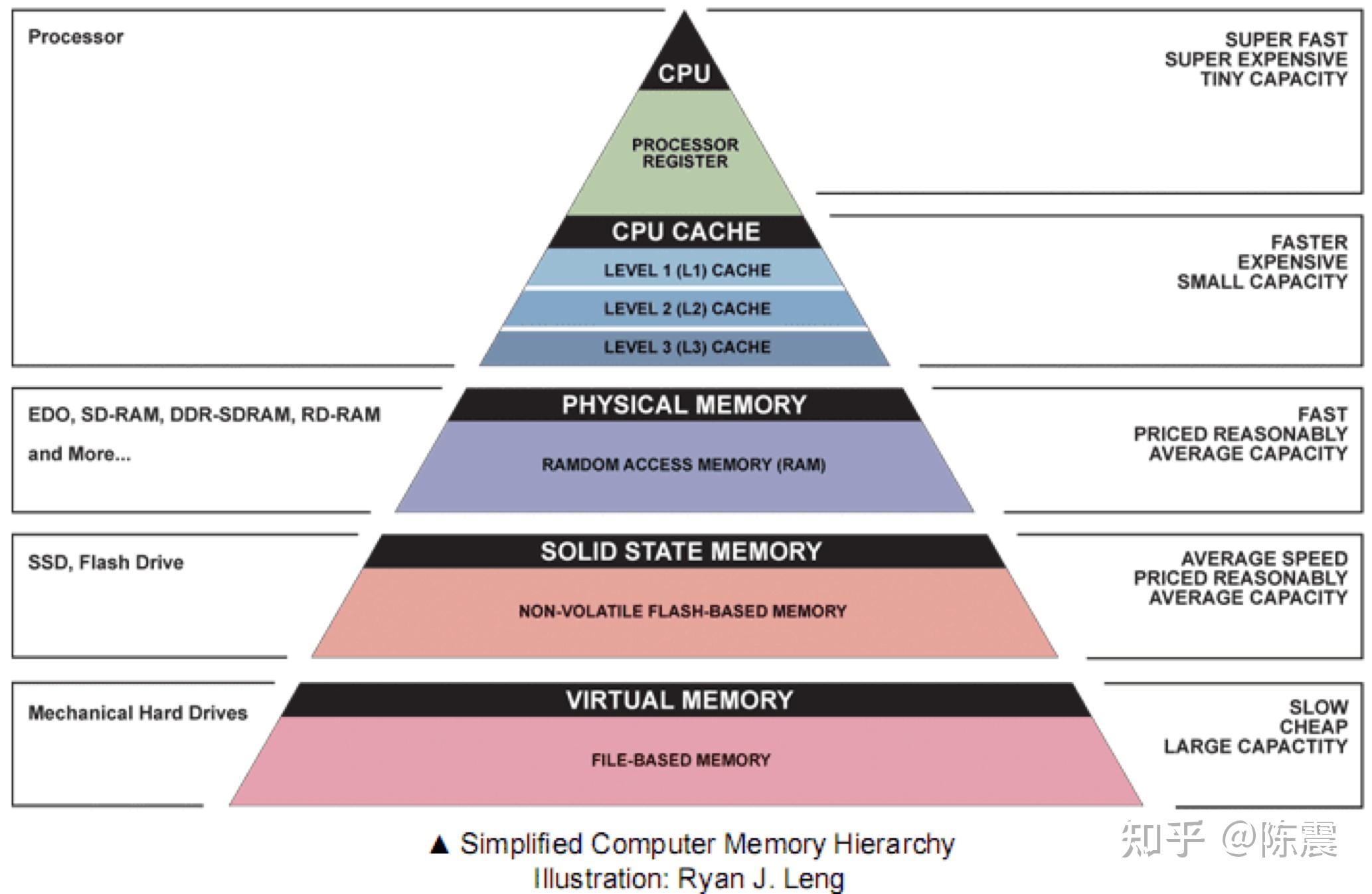
那么从内存的角度，我们能优化哪些？首先我们总结几个知识点：

IO远远慢于计算，数量级上的慢
内存的随机读写远远慢于顺序读写，即便是RAM
在大多数编程语言中，都是“行优先”。也就是说我们代码中如果用了二维数组，其在内存中的真实分布是一行一行顺序拼起来的

这三个知识点跟上面的代码有什么关系？如果你观察的足够仔细就会发现，由于我们编程的习惯问题，我们的两层循环中，外层循环是X，内层循环是Y。虽然这样写代码看起来“很舒服”，但是我们的内存就“很不舒服”了，这会导致比较严重的内存随机读写的问题，如下图左边所示。

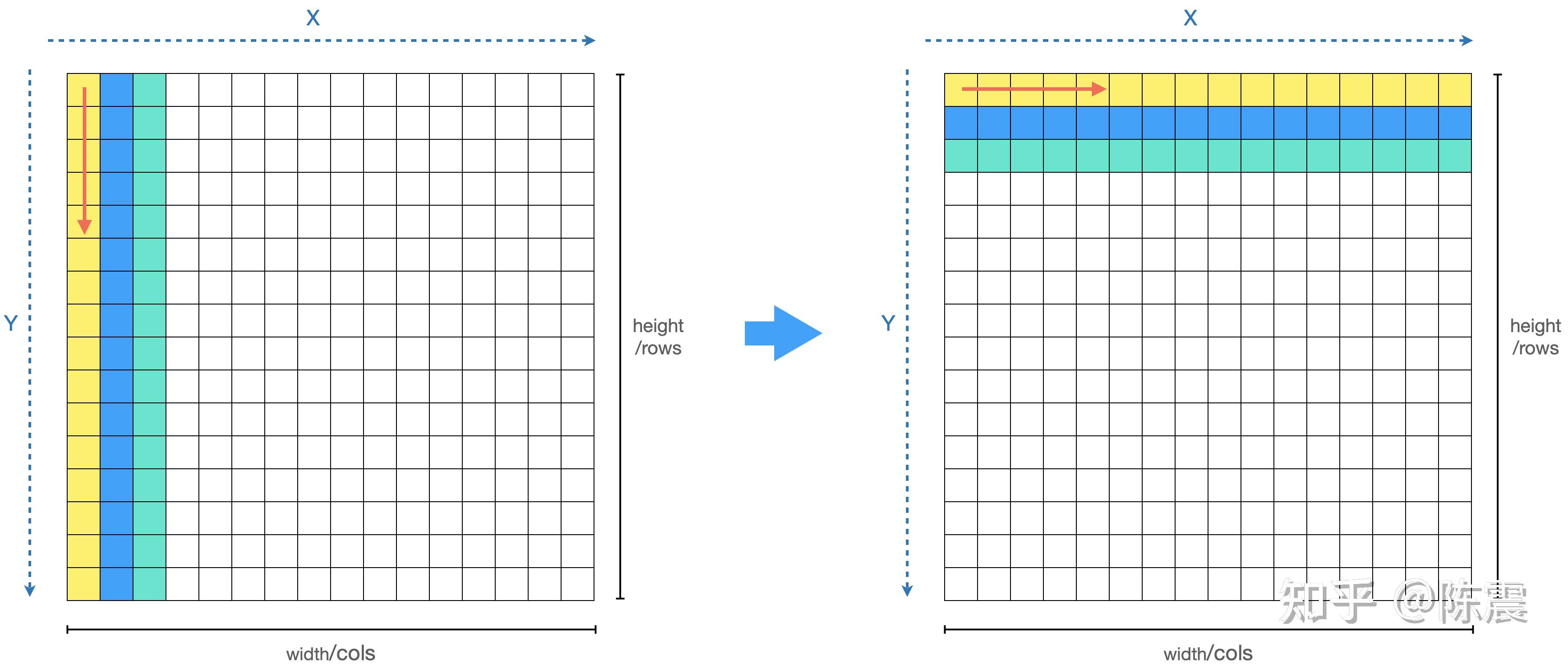
其优化方法也非常简单，我们只需要把两层循环交换一下位置。

void blur_mat_locality(const vector<vector<float>> &input,
                       vector<vector<float>> &output) {
  int height = input.size();
  int width = input[0].size();
  int right, right_right, below, below_below;
  // 交换位置
  for (int y = 0; y < height; ++y) {
    for (int x = 0; x < width; ++x) {
      right = x + 1 >= width ? width - 1 : x + 1;
      right_right = x + 2 >= width ? width - 1 : x + 2;
      output[y][x] =
          (input[y][x] + input[y][right] + input[y][right_right]) / 3;
    }
  }
  // 交换位置
  for (int y = 0; y < height; ++y) {
    for (int x = 0; x < width; ++x) {
      below = y + 1 >= height ? height - 1 : y + 1;
      below_below = y + 2 >= height ? height - 1 : y + 2;
      output[y][x] =
          (output[y][x] + output[below][x] + output[below_below][x]) / 3;
    }
  }
}

这么一个简单的操作，会有多大的性能提升呢？这次的运行时间从3281ms大幅下降到2057ms，性能提升了37%，相较于最原始的做法，几乎提升了一倍！

如果一个应届生同学的面试能优化到这个程度，应该可以拿到Offer了吧：）

注意：为了简化编程，代码中用vector<vector<float>>表示矩阵，因此，矩阵的两行数据之前，在内存中可能并不是顺序排列，这更加剧了内存随机访问的开销

其实到上面，我们还没进入并行编程的部分。那么如何利用并行编程对上面的代码继续优化？我们在遍历和计算每个元素时，他们之间是“独立”的，也就是说我们可以利用CPU的多个核心，同时对多个元素进行计算，这就是并行编程最朴素思想。

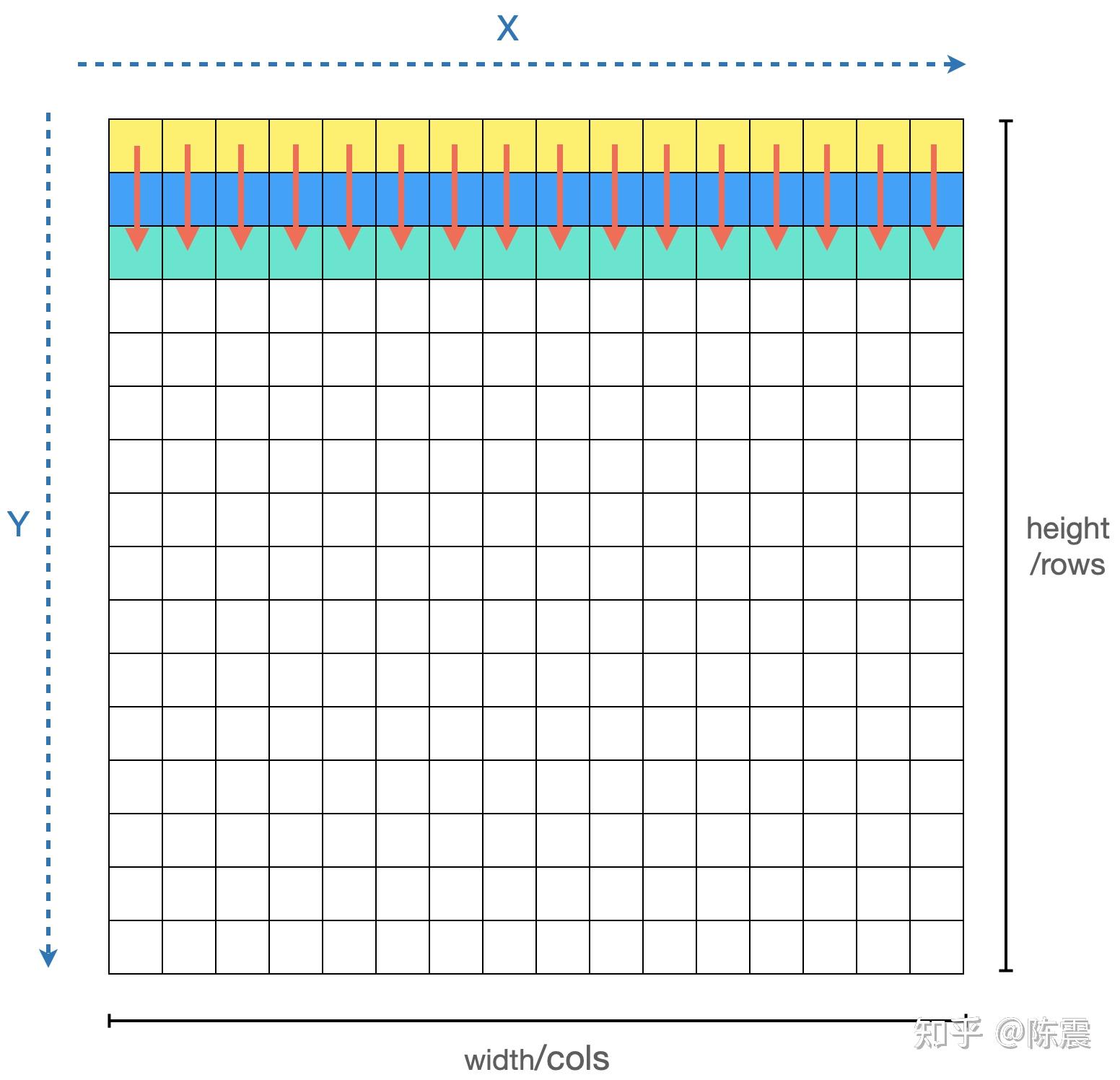
实际的编程中，我们可以利用多线程机制。如果CPU有16个核，那么我们可以同时启动16个线程，每个线程负责矩阵中的一列或者一行数据的计算（应该优先用列还是行？大家可以思考一下）。多线程编程不是本文的重点，我们直接介绍一种更简单的方法：OpenMP。

Home

OpenMP是一个开源的并行计算模型和接口，通过提供一系列的编译级别的指令，大大简化了CPU上并行编程的难度。关于OpenMP的详细介绍，大家可以关注官网或者其他资料，这里不再赘述。回到我们的问题本身，我们只需要在代码中增加一行，就可以利用CPU的多核实现并行计算：

void blur_mat_parallel(const vector<vector<float>> &input,
                       vector<vector<float>> &output) {
  int height = input.size();
  int width = input[0].size();
  #pragma omp parallel for
  for (int y = 0; y < height; ++y) {
    int below = y + 1 >= height ? height - 1 : y + 1;
    int below_below = y + 2 >= height ? height - 1 : y + 2;
    for (int x = 0; x < width; ++x) {
      int right = x + 1 >= width ? width - 1 : x + 1;
      int right_right = x + 2 >= width ? width - 1 : x + 2;
      output[y][x] =
          ((input[y][x] + input[y][right] + input[y][right_right]) +
           (input[below][x] + input[below][right] + input[below][right_right]) +
           (input[below_below][x] + input[below_below][right] +
            input[below_below][right_right])) / 9;
    }
  }
}

这里我们使用了OpenMP中的指令#pragma omp parallel for，这条指令告诉编译器，接下来的这个for循环，请帮我使用多线程进行并行计算。由于使用了编译指令，因此gcc在编译这段代码的时候，对会循环中y的每一个值在一个线程中运行从而实现并行加速。当然，OpenMP假设接下来的这些循环之间是“独立”的，且不会保证多个循环之间的执行顺序问题，这些都需要程序员自己去保证。

为了能成功编译，需要额外添加一个编译选项-fopenmp。

$ g++ cpu.cpp -O0 -o cpu -std=c++11 -fopenmp && https://zhuanlan.zhihu.com/p/cpu

经过这样的优化，我们这段代码的运行时间是多少呢？182ms！相较于最朴素的实现，我们整整提升了21.5倍，这就是并行编程的威力。

细心的同学可能发现了，上面的这段代码中仍然有重复计算的部分，我们为什么没有把第三章中的优化方法也用上呢？我们试试看。

void blur_mat_parallel_redup(const vector<vector<float>> &input,
                             vector<vector<float>> &output) {
  int height = input.size();
  int width = input[0].size();
  #pragma omp parallel for
  for (int y = 0; y < height; ++y) {
    for (int x = 0; x < width; ++x) {
      int right = x + 1 >= width ? width - 1 : x + 1;
      int right_right = x + 2 >= width ? width - 1 : x + 2;
      output[y][x] =
          (input[y][x] + input[y][right] + input[y][right_right]) / 3;
    }
  }
  // can not parallel here ！！！
  for (int y = 0; y < height; ++y) {
    for (int x = 0; x < width; ++x) {
      int below = y + 1 >= height ? height - 1 : y + 1;
      int below_below = y + 2 >= height ? height - 1 : y + 2;
      output[y][x] =
          (output[y][x] + output[below][x] + output[below_below][x]) / 3;
    }
  }
}

由于把一个循环变成两个循环，我们需要用两次OpenMP的编译指令。但是仔细观察就会发现，第二个循环体在计算过程中，需要同时读output和写output矩阵且多个线程之间的读写操作存在交集。当多个线程同时且随机地对output进行操作时，由于这里没有锁机制，会出现严重的不一致问题，从而影响计算结果的正确性。那上面的这种写法实际效率如何？大约在1115ms左右，远远慢于刚刚的182ms。

如果一个应届生同学能回答到这个程度，应该会拿到一个不错的 Offer了：）

那有没有什么方法，可以同时利用多线程加速并且消除重复计算呢？肯定有，那就是Tiling分片计算方法。上一章节的实现之所以会出现错误主要有两个因素。一是因为存在了两个循环，因此不得不两次使用OpenMP的编译指令；二则是因为output变量在多个线程之前存在了同时读写的问题。Tilling的中文含义是“瓷砖”，也就是说，我们把原始数据像铺瓷砖一样“一大片一大片”的处理。

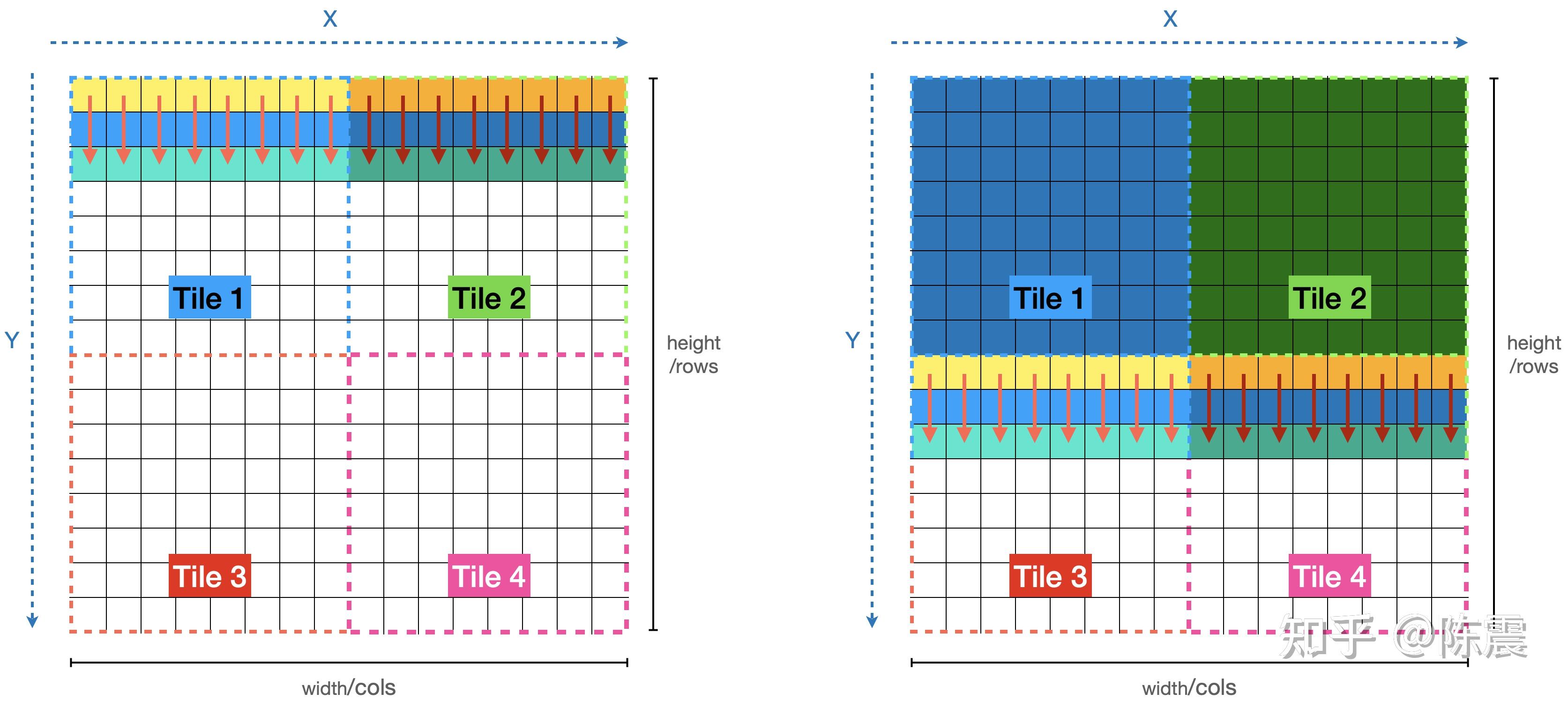
如上图所示，我们可以把原始数据分片成四份，四个分片可以并行，分片内部也可以按照之前的方法并行。看代码：

void blur_mat_tiling_parallel(const vector<vector<float>> &input,
                              vector<vector<float>> &output, int tile_width, int tile_height) {
  int height = input.size();
  int width = input[0].size();
  #pragma omp parallel for
  for (int tile_y = 0; tile_y < height / tile_height; ++tile_y) {
    int t_y = tile_y * tile_height;
    for (int tile_x = 0; tile_x < width / tile_width; ++tile_x) {
      int t_x = tile_x * tile_width;
      vector<vector<float>> tile_tmp(tile_height, vector<float>(tile_width, 0));
      for (int y = 0; y < tile_height; ++y) {
        int target_y = t_y + y;
        for (int x = 0; x < tile_width; ++x) {
          int target_x = t_x + x;
          int right = target_x + 1 >= width ? width - 1 : target_x + 1;
          int right_right = target_x + 2 >= width ? width - 1 : target_x + 2;
          tile_tmp[y][x] = (input[target_y][target_x] + input[target_y][right] +
                            input[target_y][right_right]) / 3;
        }
      }
 
      for (int y = 0; y < tile_height; ++y) {
        int target_y = t_y + y;
        int below = y + 1 >= tile_height ? tile_height - 1 : y + 1;
        int below_below = y + 2 >= tile_height ? tile_height - 1 : y + 2;
        for (int x = 0; x < tile_width; ++x) {
          int target_x = t_x + x;
          output[target_y][target_x] =
              (tile_tmp[y][x] + tile_tmp[below][x] + tile_tmp[below_below][x]) / 3;
        }
      }
    }
  }
}

现在，代码貌似变得复杂了一点，别慌。改动就两点：

把原来的两次循环改成了四层循环，从而可以在分片维度实现并行，比如在第5行，我们可以在最外层的循环使用OpenMP的编译指令
在第10行，我们为每个分片增加了一个临时存储空间，在减少重复计算的同时，避免上一章中提到的多线程同步的问题

这个过程，看一个动画会更容易理解。

图自Vectorize, parallelize, unroll and tile your code (halide-lang.org)

经过这样的优化，性能是多少呢？同样的参数和硬件配置下，这个实现是231ms，貌似并没有比之前的更好。至于为什么，我没做深入的profile所以不好确认。我猜测是更复杂的循环和临时空间的使用，都影响了实际执行的性能。这也告诉我们性能优化在很多时候并不是把“十八般武艺”都用上就会更好。

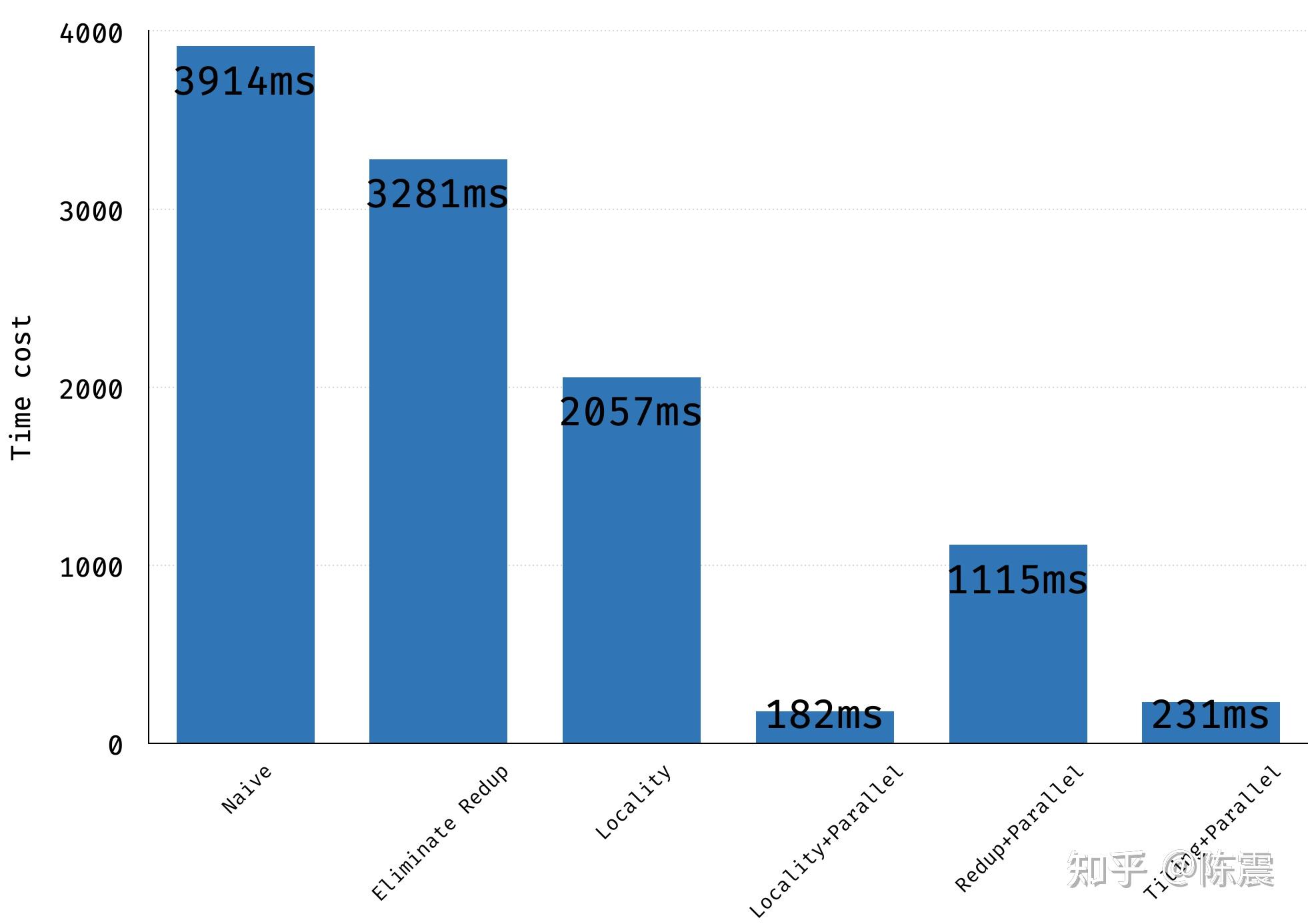
到这里，我们从消除重复计算；内存连续性和并行计算三个方面对代码进行了优化，执行时间从3914ms大幅下降到200ms一下，提升了近20倍。

除了上面提到的三种优化，还有没有其他手段？该轮到大杀器“指令集优化”出场了。

我们知道，CPU的计算都被抽象成了一系列的CPU指令集，有些指令集负责从内存加载数据到寄存器，有些指令集则从寄存器读取数据执行具体的计算操作，然后再由另外一些指令集把寄存器中的数据更新回内存。不同的CPU架构和指令集能操作的数据大小是不同的，从16bit，32bit到64bit。在同样的计算精度下，能操作的数据量越大就代表了计算的“吞吐”越大，也就表示更快的计算速度。这正是SIMD的初衷。

Single Instruction Multiple Data指的就是CPU在硬件上，支持一个指令读写一个向量(128bit)，更重要的是，可以对两个向量同时执行计算且计算是可分割的。也就是说可以把128bit看成4个32bit的float分别对4个float执行同样的计算。举个例子，如果我们要计算四对数的和：

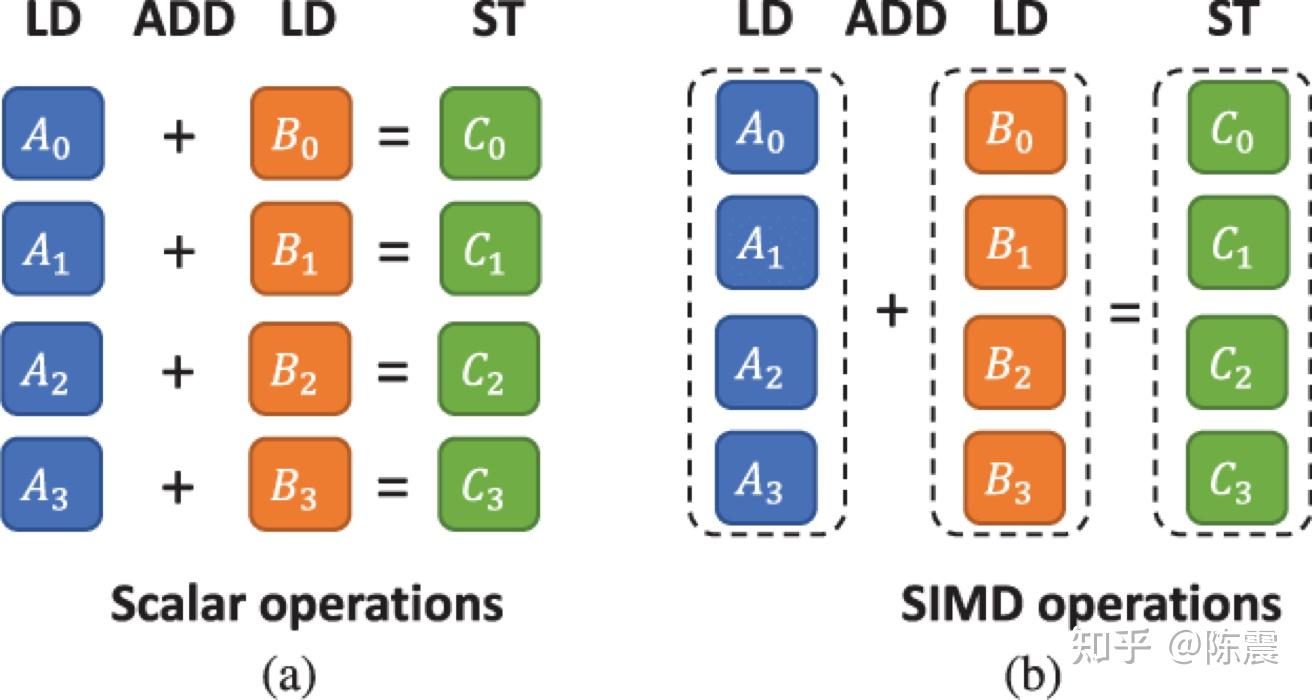
在没有用SIMD时，我们首先需要八次LD操作用来从内存把数据加载到寄存器；然后用四次ADD操作执行加法计算；最后再用四次ST操作，把计算结果存储到内存中，故共需要16次CPU指令操作。

如果用SIMD，我们首先需要一次LD操作一次性把四个数据加载到寄存器；然后执行一次ADD操作完成加法计算；最后用一次ST操作把数据更新回内存，这样只需要3次CPU指令操作。相较于第一种方法性能提升了5倍之多，下图则从另外两个角度展示了SIMD的优势。

目前绝大多数的CPU都支持SIMD，那如何使用SIMD能力？不同的CPU架构和厂商提供了不同的SIMD指令集来支持，以我们常用的x86架构来说，我们可以通过SSE指令集来使用x86架构下的SIMD能力。

这篇文章内容有点长了，关于如何在代码中使用SIMD和SSE指令集，我们放到下一篇中介绍。

本文涉及的代码，见：

zackchen/ParallelProgrammingInAction

参考资料