- 手机:138 0000 0000
- 传真:+86-123-4567
- 全国服务热线:400-123-4567


原文链接:
ORCA优化器浅析大家好,我是 「微扰理论」。目前在 hashdata 担任数据库内核研发工程师,感兴趣的同学可以通过文末联系方式找我内推哦。入职即享20天年假,优秀更可远程办公,海量HC等你来投。感兴趣也可以通过之前的文章「如何心算多位数乘法」了解我组日常沟通氛围。 微扰酱也是极客时间专栏 《业务开发算法50讲》 的作者;欢迎大家关注。
微扰酱最近因为工作需要,学习了一下 ORCA 的论文 《Orca: A Modular Query Optimizer Architecture for Big Data》,这里记录一下学习笔记;重点将会放在 ORCA 的优化过程上,这也是最近工作中最需要了解的部分。
ORCA 是 Pivotal 开源的一款基于 Cascades 框架的数据库优化器,当时也应该是世界上唯一一个开源的、与数据库主体独立的、可服务于多个不同数据库产品的查询优化器。项目应该是11年就开始开发,论文则是在16年正式发布,至今已经走过了10个年头。
当然,所谓服务多个不同数据库产品,其实到目前为止也只是支持了 Pivotal 公司旗下的 HAWQ 和 Greenplum 两个产品而已,如果需要支持其他数据库,则需要针对算子、元数据等差异进行适配,工作量也相当不小。据我所知,似乎没有什么公司基于 ORCA 实现了其他数据库的优化器。
而目前,Greenplum 自身的很多查询也需要 fallback 到 pg 的优化器才能生成查询计划,在 GPDB 内核升级了若干个版本之后,ORCA 在功能上来说已经不够完备,社区活跃相比于刚开发的时候有所下降。不过 ORCA 依旧是 Cascades 架构的一个非常优秀的开源实现,被工业界广泛参考,值得对优化器感兴趣的同学好好学习一下。
站在巨人的肩膀上,ORCA 在一开始设计的时候,就考虑的比较充分,提供了以下一些特性:
最终,ORCA 带着 Cascades 框架与生俱来的优势,在 Pivotal 当时的系统上获得了非常显著的性能提升。
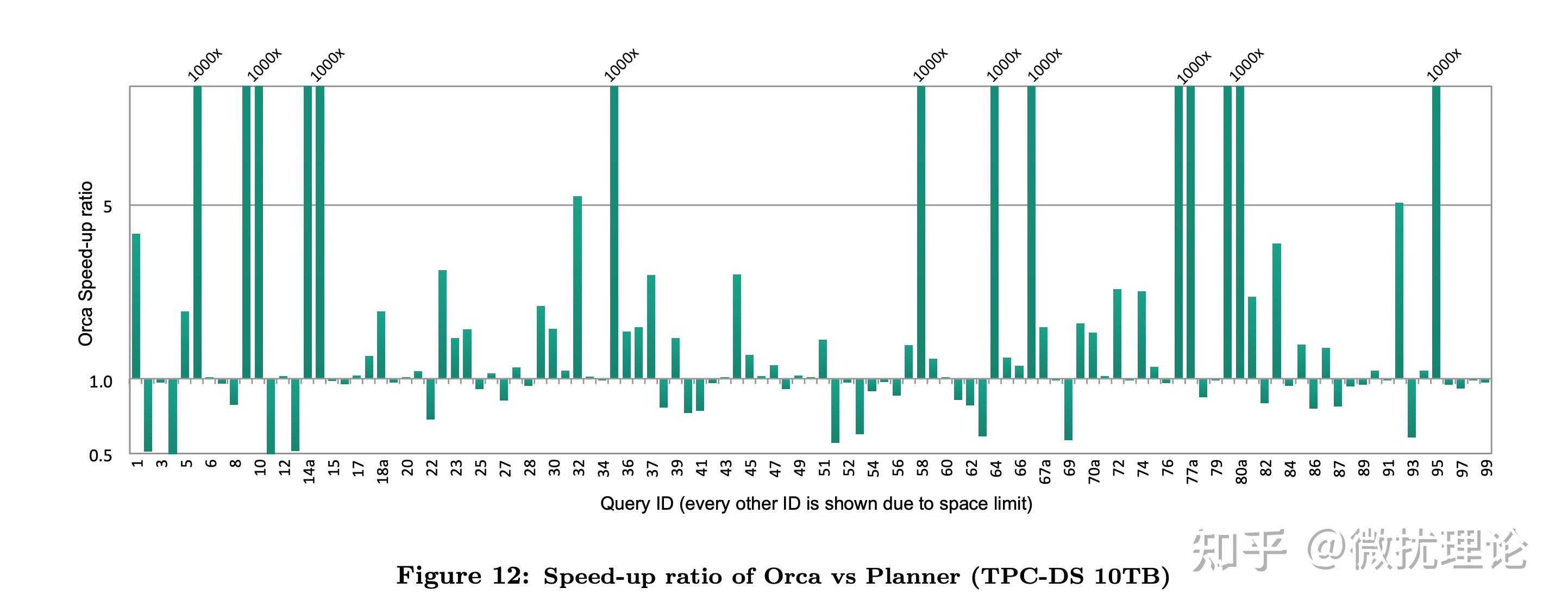
我们前面提到,在 ORCA 以前,几乎所有的优化器都是和数据库系统耦合在一起的;而 ORCA 希望能适配更多的数据库,自然首先要对和数据库系统交互的接口进行抽象和设计。

DXL 正是为了这一目标而设计的,通过定义了一系列基于XML语言的语法,ORCA 可以通过接口获得查询树和源数据的相关信息,也可以将优化好的查询计划通过接口提供给数据库系统进行执行。不同的数据库原则上只需要提供对 Query2DXL\\MD Provider\\DXL2Plan 这几个模块的适配和实现即可让 ORCA 成为该数据库的优化器了,所有的信息都会通过 DXL 的方式进行交互。
这也天然得让 ORCA 的测试变得简单,其独立部署的特性,让我们只需要提供文本格式的 DXL 文件,就可以模拟查询语句的输入,而无需启动整个数据库系统。校验的时候则只需要比对输出的 DXL 计划是否符合预期即可。
ORCA 论文中将架构分为了6个部分,分别是 Memo, Seach and Job Scheduler, Transformation, Property Enforcement, Metadata Cache 和 GPOS。
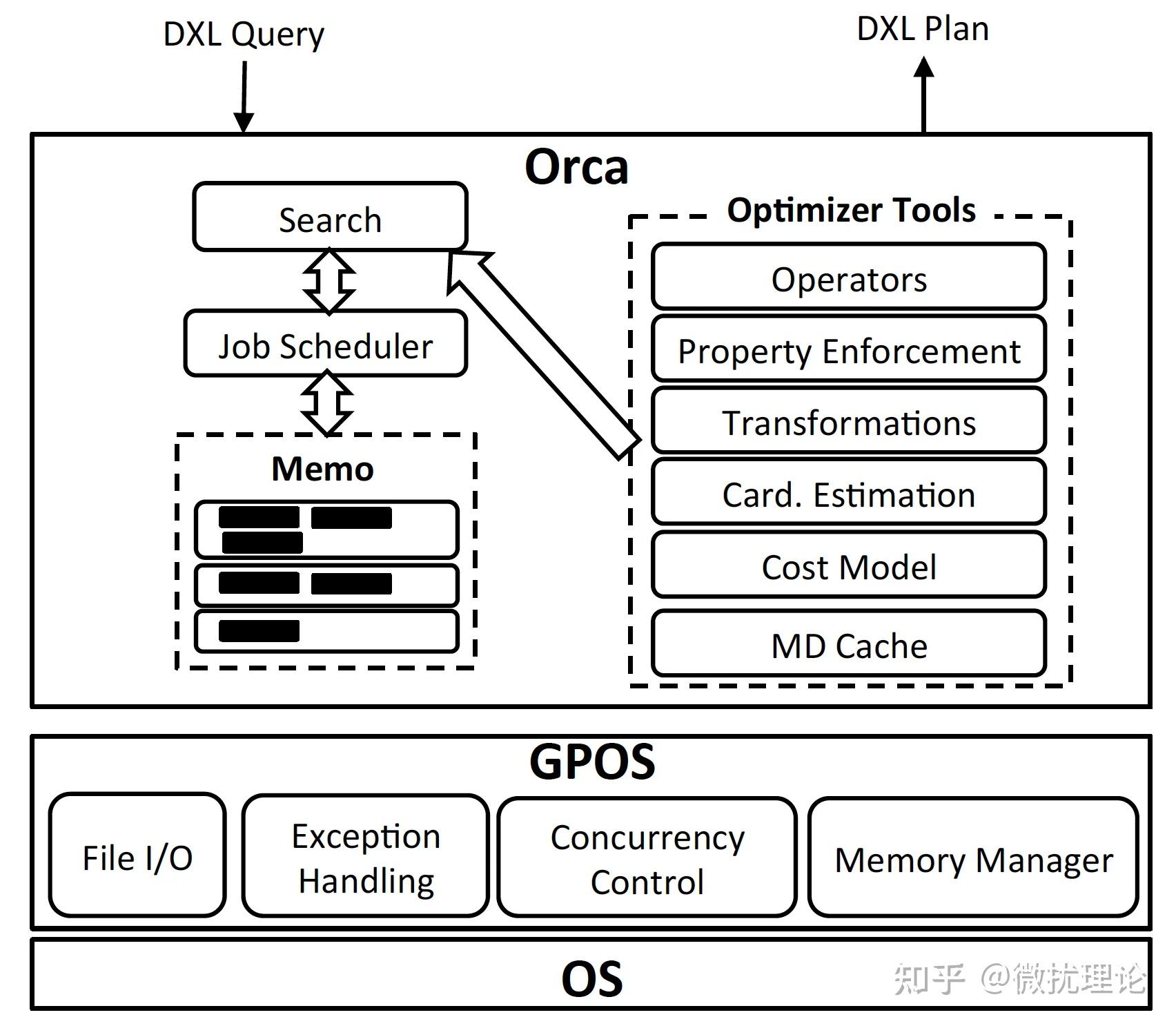
对于这样的架构划分微扰酱其实是觉得有点奇怪的,比如 Search 和 Transformation 在我看来就不是边界清晰的独立部分;不过我们还是按照原作的意思简单阐述一下。
其中,GPOS 是为了适配不同操作系统的抽象层, Metadata Cache 则是由于元数据变动不频繁特性所引入的缓存层;比较独立,和优化过程关系不大,就不展开讨论了。
Memo,是 ORCA 中用于表示执行计划搜索空间的数据结构,应该是 Cascades 架构的核心所在;和 pg 传统采用的优化器自底向上动态规划寻找最优解的方式不同, Cascades 架构则采用了类似于自顶向下记忆化搜索的策略,相比于自底向上的方式也可以更有效的进行减枝从而在有限的时间里获得更优的方案。 Memo 将整个执行计划搜索空间表示为一系列 Group; 每个 Group 则由执行计划中的一组逻辑上等同的算子表达式构成,在搜索的过程中,新的 Group 可能会被创建,新的算子表达式也可能被添加到 Group 中;我们在讲解优化过程的时候将展开讨论。
Seach and Job Scheduler,本质上描述的是 ORCA 搜索最优计划的过程。如前文所述, ORCA 设计了一个非常不错的调度器,在有依赖关系的计划中,进行并行的搜索工作。整个搜索的过程则由几个部分构成,分别是 exploration\\implementation\\optimization 。其中 exploration 负责根据优化规则补全逻辑上等价的算子表达式,比如 a join b 和 b join a 就是等价的。 而 implementation 则是负责将逻辑算子转化为物理算子,比如 a join b 在物理上既可以是 hashjoin 也可以是 nested loop join 还可以是 merge join。 最后一步则是 optimization, 会将数据属性要求(排序和分布)通过增加算子的方式加到计划上并进行最后的代价估计。
Transformation,其实就是 Search 过程中 exploration 和 implementation 的主要逻辑,基于优化规则对搜索空间进行补全。这里的优化规则,就是指的 Transformation,如 InnerJoin(A, B) -> InnerJoin(B, A) 或者 Join(A, B) -> HashJoin(A, B) 等。
Property Enforcement,则就是前面说的 optimization 里的一步。 在我们的查询语句或者执行计划的节点中可能会要求数据按照某种方式分布,或者按照某些字段排序;这些要求,就是 Property,我们不时需要添加一些算子,去使得数据按照要求的属性排布。这一步显然需要在最后的代价估算之前完成。
现在我们来聊一聊大部分读者最关心的部分, ORCA 优化 SQL 语句的具体步骤;后续讲解都将基于下述例子展开。
SELECT T1.a From T1, T2
WHERE T1.a=T2.b
ORDER By T1.a;
我们知道任何一条语句首先当然是传递给数据库系统的;在 ORCA 中,我们会复用数据库(Greenplum)对语句的解析能力,而要求数据库系统讲解析树以 DXL 的格式传递给 ORCA;因此我们也就得到了可以认为是未被优化的 SQL 语句逻辑表达式和 copy-in 初始化的 Memo 结构体,显然也是一个树状的结构。
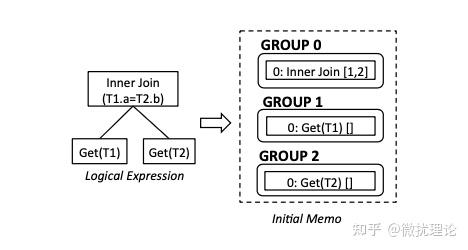
例子中SQL语句所对应的逻辑表达式和初始化的 Memo 如图所示;其中 Group 之间的依赖关系是通过算子间的引用关系所描述的。在例子中, Group 0 中的 InnerJoin[1,2]就代表着 Group 1 和 Group 2 是 Group 0 的子表达式。
在 Memo 被初始化完毕之后,我们就会马上开始优化的过程,具体来说包含以下四个步骤:Exploration\\Statistics Derivation\\Implementation\\Optimization;我们逐一讲解。
其实这一步前面已经简单提过,就是对逻辑等价的算子的扩展,目的是补全搜索空间;这一步完成后,意味着 Memo 应该存储着指定 SQL 语句所对应的完整逻辑搜索空间。而具体的过程,就是对每一个 Group 的表达式进行规则的匹配和应用,以添加新的表达式到某个 Group 或者创建新的 Group。 比如前面说的 InnerJoin[1,2]-> InnerJoin[2,1] 就对应着规则 CXformJoinCommutativity。
我们知道,对算子估计代价的时候,我们需要知道一些表的数据分布情况,比如每个表有多少行数据,对于某一列来说不同的值又有多少行数据等等。这些信息,通常采用对表进行数据直方图的统计来估计,目的是为了估算基数和数据倾斜。这一步骤则正是在优化的过程中,为 Memo 中的 statistics object 绑定上合适的估计值,以便于之后估计最终的执行代价;显然,在这个步骤中不会导致 Memo 搜索空间的变化。
整个获取统计信息的过程比微扰酱想象中的要复杂一些,分为自顶向下和自底向上两个阶段。

首先,我们会从根节点往下分发信息统计的请求,直到叶子节点。每个 Group 会且仅会存在一个 statics object。而计算统计信息的时候,其实同一个 Group 下的不同表达式估计出来的结果很可能是不同的;以 InnerJoin 为例,在有多个不同的 Join 顺序时,带有更少的 Join 条件的表达式比带有更多的 Join 条件的表达式的直方图信息会更靠谱一些,我们每次求解某个 Group 的统计信息时,都会选择最靠谱的算子进行估计。然后,当子节点的统计信息绑定完成之后,父节点就会组合子节点的统计信息并绑定到父节点的 Group 中,直至自底向上完成所有节点统计信息的绑定。
理解了 Exploration 的过程之后,Implementation 的过程就很好理解了,本质上都是对 Transformation 的应用。两者主要的区别在于这次我们触发和应用的规则都是用于创建物理执行算子的。 比如 CXformInnerJoin2NLJoin 和 CXformInnerJoin2HashJoin 被触发时就会产生 Hash Join 和 Nested Loop Join 的物理算子。
最后一步,则是优化了。事实上,在以上三步里,ORCA 并没有很体现出其 MPP 环境下特有的属性,在这一步里则终于会有所体现。 如前文所述,一些算子和我们的查询本身都可能会有对数据分布和有序性的要求;比如在本文的例子中,我们就要求最终的数据按照 T1.a 列进行排序,或者对于 HashJoin 这样的算子来说,我们显然会要求在 MPP 环境下,被 Join 的两张表需要按照 Join 的列哈希分布,这样才能保证会被 Join 条件命中的两表中的数据一定都分布在同一台机器上。
这样的要求我们会通过自顶向下传递优化请求的方式在 Memo 中通过添加部分算子的方式得以满足,这一步被称为 Property Enforcement。比如为了满足排序的要求,我们就会添加 Sort 算子;而为了使得数据分布正确,我们可能会引入 Redistribute 算子。 优化请求会不断的往下传递,每次向下传递的优化请求对数据分布和排序的要求会同时取决于算子收到的优化请求,也会取决于当前算子的要求;而这些信息,我们都会在每个 Group 和每个算子表达式中通过哈希表的方式进行维护,这样计算过的结果也不必被重复计算。在算子的哈希表下,算子之间的依赖关系也通过和 Request 的引用关系维护起来了,具体可以看后面的例子。
而在 Group 下的哈希表中,每个请求都会和当前最优的算子表达式绑定。这里所谓的最优是代价模型利用前述统计信息所估计的代价最小,具体过程在论文中没有展开讲解,等微扰酱看懂代码之后可能还会再撰文讨论。

针对前面的例子,论文中实际上给了一个非常具体的示意图,从 Group Hash Table 中的第一个优化请求#1开始,可以依次串联 GExpr 8: GatherMerge -> Request 3 -> GExpr 6: Sort -> Request 4 -> GExpr 4: Inner HashJoin ->{Request 7, Request 10}...,直至描述出完整的最优执行计划。 ORCA 论文对这个例子有非常具体的讲解,迷惑的同学可以对照论文进一步了解。
论文还花费不少笔墨阐述了并行执行优化实现、元数据交换、可验证性和实验等部分;感兴趣的同学可以自行阅读论文了解。
应该是入坑数据库以来第一篇关于数据库内核的文章,虽然只看了论文还未深入代码细节,但写完还是很开心的,希望未来可以更稳定地输出更多和数据库相关的文章;欢迎大家持续关注,不妨点个关注吧。
微扰酱也正在组织各种「残酷的」学习打卡活动,比如 CSAPP 阅读打卡活动就正在火热进行中!想来一起组队刷 coursera 或者 leetcode 的话可以关注公众号;菜单中也有微扰酱的联系方式。
我们的团队人数
我们服务过多少企业
我们服务过多少家庭
我们设计了多少方案