- 手机:138 0000 0000
- 传真:+86-123-4567
- 全国服务热线:400-123-4567


正弦余弦算法(Sine cosine algorithm,简称SCA)是2016 年由澳大利亚学者Seyedali Mirjalili 提出的一种新型仿自然优化算法[1]。该算法通过创建多个随机候选解,利用正余弦数学模型来求解优化问题,具有结构简单、参数少、易于实现的特点,但也存在优化精度低、容易陷入局部极值、收敛速度慢等问题。
一般而言,基于总体的优化技术以一组随机解开始优化过程。该随机集通过目标函数反复评估,并通过作为优化技术核心的一组规则进行改进。由于基于总体的优化技术是随机寻找优化问题的最佳方法,因此无法保证一次运行即可找到解决方案。但是,有了足够多的随机解和优化步骤(迭代),找到全局最优解的可能性就会增加。
不管基于随机种群的优化领域中算法之间的差异如何,常见的是将优化过程分为两个阶段:探索与开发。在前一阶段,优化算法将解集中的随机解与高随机率的随机解相结合,寻找搜索空间中有希望的区域。但是在开发阶段,随机解是逐渐变化的,随机变化远小于探索阶段的变化。

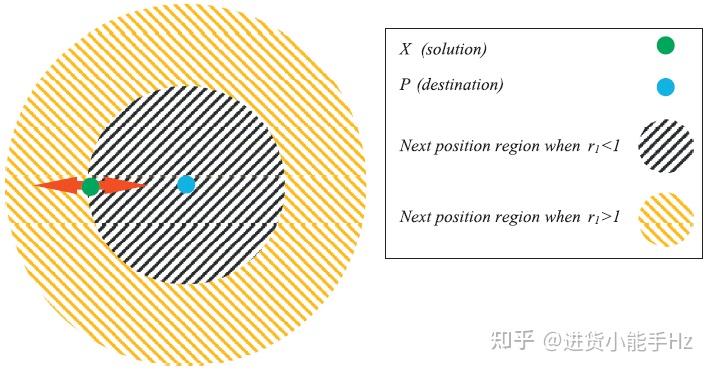
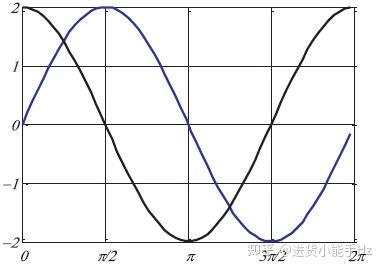
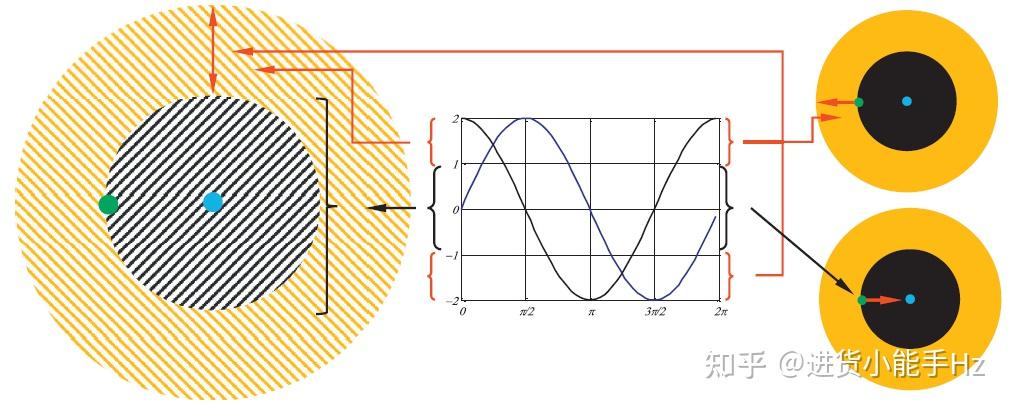


选取2个测试函数来评估SCA算法性能,其形式如表2-1所示。测试函数的3D图,如图2-4所示。测试函数收敛曲线变化过程,如图2-5所示。其中SCA算法搜索得到的最佳解以及最佳适应值,如表2-2所示。

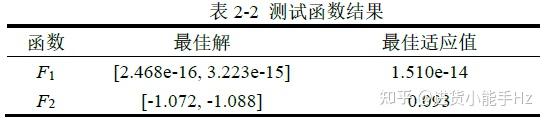
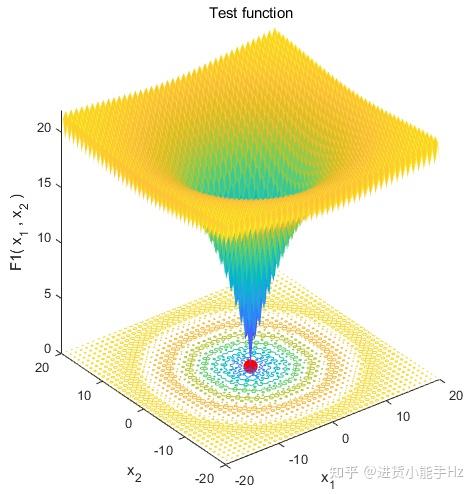
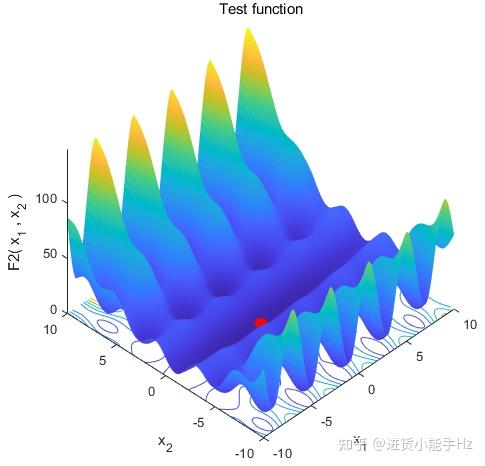
图2-4 测试函数 SCA寻优 3D图
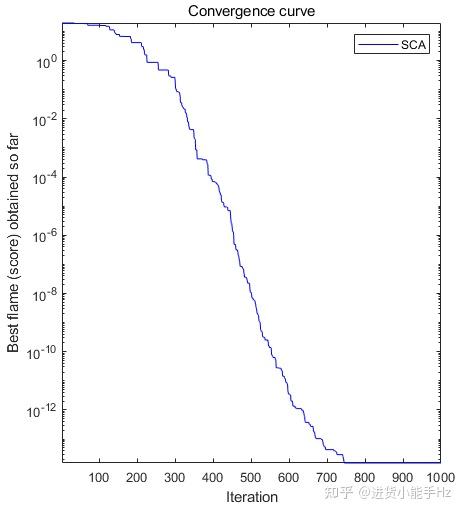
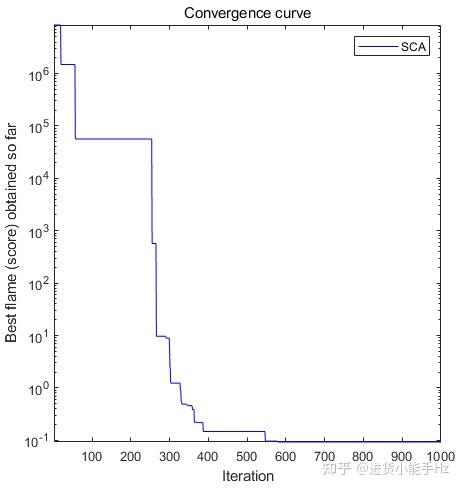
图2-5 测 试函数收敛曲线
测试函数的结果表明,该算法的收敛速度较快,且具有高探索性和局部最优避免性。从组合测试函数的结果来看,该算法也能够成功地平衡探索和开发,以确定具有挑战性的测试函数的全局最优解。性能度量的结果证明,SCA要求其搜索代理在优化的初始阶段突然改变,在优化的最后阶段逐渐改变。结果表明,这种行为导致了对搜索空间的广泛探索和对最有前途区域的开发。
[1]Mirjalili S . SCA: A Sine Cosine Algorithm for Solving Optimization Problems[J]. Knowledge-Based Systems, 2016, 96.
[2]石磊(Bonacci Shi). 一种改进的正弦余弦优化算法[D]. 武汉大学, 2018.
我们的团队人数
我们服务过多少企业
我们服务过多少家庭
我们设计了多少方案