- 手机:138 0000 0000
- 传真:+86-123-4567
- 全国服务热线:400-123-4567


pdf下载地址:最优化方法期末考试复习
最优化理论与方法知识点总结 1
一、最优化简介: 2
1.1最优化应用举例 2
1.2基本概念 2
1.3向量范数 3
1.4矩阵范数 3
1.5极限的定义 3
1.6方向导数存在性和计算公式 4
1.7梯度定义 4
1.8海塞矩阵 5
1.9泰勒展开式: 5
1.10凸集定义 5
1.11凸集性质 5
1.12凸函数定义 6
1.13凸函数判断 6
1.14矩阵正定与半正定判断 6
1.15例题(判断矩阵是否正定) 7
1.16凸优化 7
二、线性规划 7
2.1线性规划数学模型的一般形式 7
2.2解的基本定理 7
2.3解的分类 8
2.4图解法 8
2.5例题(图解法) 8
2.6标准型的化法 9
2.7例题(化为标准型) 9
2.8单纯形法 10
2.9例题(单纯形法) 11
三、对偶线性规划 13
3.1对偶问题 13
3.2单纯形法解对偶问题 13
3.3对偶单纯形法求解线性规划问题过程 14
四、无约束优化 14
4.1无约束优化概述 14
4.2搜索区间的确定 15
4.3区间消去法原理 16
4.4黄金分割法 17
4.5插值方法 17
4.6常见的终止准则 19
4.7最速下降法 20
4.8牛顿类方法 20
4.9例题(牛顿类方法) 21
1.1最优化应用举例
具有广泛的实用性 运输问题,车辆调度,员工安排,空运控制等 工程设计,结构设计等 资源分配,生产计划等 通信:光网络、无线网络,ad hoc 等. 制造业:钢铁生产,车间调度等 医药生产,化工处理等 电子工程,集成电路VLSI etc. 排版
1.2基本概念
目标函数和约束函数都是线性的,称之为线性规划问题,而有的模型中含有非线性函数,称之为非线性规划。 在线性与非线性规划中,满足约束条件的点称为可行点,全体可行点组成的集合称为可行集或可行域。如果一个问题的可行域是整个空间,则称此问题为无约束问题. 最优化问题可写成如下形式:
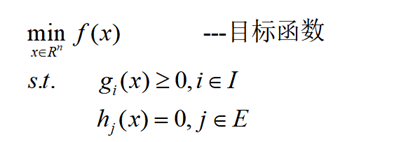

1.3向量范数
1-范数:║x║1=│x1│+│x2│+…+│xn│
2-范数:║x║2=(│x1│2+│x2│2+…+│xn│2)1/2
∞-范数:║x║∞=max(│x1│,│x2│,…,│xn│)
1.4矩阵范数
1-范数:
║A║1 = max{ ∑|ai1|,∑|ai2|,……,∑|ain| } (列和范数,A每一列元素绝对值之和的最大值)(其中∑|ai1|第一列元素绝对值的和∑|ai1|=|a11|+|a21|+…+|an1|,其余类似);
2-范数:
║A║2 = A的最大奇异值 = (max{ λi(AHA) }) 1/2 (谱范数,即A^HA特征值λi中最大者λ1的平方根,其中AH为A的转置共轭矩阵);
∞-范数:
║A║∞ = max{ ∑|a1j|,∑|a2j|,…,∑|amj| } (行和范数,A每一行元素绝对值之和的最大值)
1.5极限的定义
定义:如果序列{xn}与常数a 有下列关系:对于任意给定的正数ε(不论它多么小),总存在正整数N ,使得对于n >N 时的一切xn,不等式|xn-a |<ε都成立,则称常数a 是序列{xn}的极限。
1.6方向导数存在性和计算公式

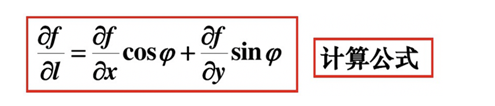
1.7梯度定义

1.8海塞矩阵

1.9泰勒展开式:
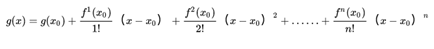
1.10凸集定义
对于n维空间中点的集合C,如果对集合中的任意两点x和y,以及实数0≤θ≤1,都有: θx+(1-θ)y∈C,则称该集合称为凸集。
1.11凸集性质
1、多个凸集的交集还是凸集 2、如果每个等式或者不等式约束条件定义的集合都是凸集,那么这些条件联合起来定义的集合还是凸集 3、凸集的并集并一定不是凸集
1.12凸函数定义
在函数的定义域内,如果对于任意的x和y,以及实数0≤θ≤1,都满足如下条件: 则函数为凸函数。当式子中不含等号时,则为函数为严格凸函数。
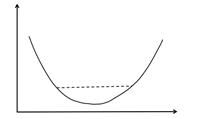
1.13凸函数判断
一阶判定规则为:
对于一元函数,凸函数的判定规则为其二阶导数大于等于0。
对于多元函数,如果它是凸函数,则其Hessian矩阵为半正定矩阵。
1.14矩阵正定与半正定判断
(1)A是n阶方阵,如果对任何非零向量x,都有xTAx>0,其中表示xT的转置,就称A为正定矩阵。
(2)A是n阶方阵,如果对任何非零向量x,都有xTAx≥0,其中表示xT的转置,就称A为正定矩阵。
1.15例题(判断矩阵是否正定)

1.16凸优化
如果一个最优化问题的可行域是凸集,并且目标函数是凸函数,则该问题为凸优化问题。Minf(x),x∈C,其中x为优化变量;f为凸目标函数;C是优化变量的可行域,是一个凸集。
pdf下载地址:最优化方法期末考试复习
我们的团队人数
我们服务过多少企业
我们服务过多少家庭
我们设计了多少方案